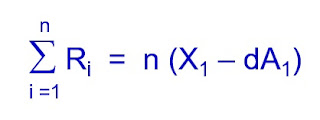วันศุกร์ที่ 6 ธันวาคม พ.ศ. 2562
LTF และความเสียเปรียบที่เราไม่เคยรู้
นับจากอดีตมาผู้ซื้อกองทุนรวม LTF หน้าใหม่มักได้รับ “คำแนะนำ” ให้ซื้อกองทุนประเภท 70/30 ซึ่งหมายถึง กองทุนจะพยายามถือครองหุ้นในสัดส่วนประมาณ 70 เปอร์เซ็นต์ และถือตราสารหนี้ เช่น พันธบัตร/เงินฝาก ในสัดส่วน 30 เปอร์เซ็นต์ที่เหลือ
คำแนะนำนี้ค่อนข้างปลอดภัยสำหรับผู้ขายกองทุน เนื่องจากกองทุนรวม LTF ประเภท 70/30 มักมีความผันผวนต่ำกว่ากองทุนรวม LTF ทั่วไป (ซึ่งลงทุนหุ้นเต็มที่) โอกาสที่ลูกค้าจะขาดทุนและกลับมาต่อว่าต่อขานในภายหลังก็มีน้อยกว่า อย่างไรก็ตาม สิ่งนี้มีความเสียเปรียบแอบแฝงอยู่
โดยธรรมชาติแล้ว กองทุนรวมที่ลงทุนหุ้นมักคิดค่าธรรมเนียมการบริหารจัดการสูงกว่ากองทุนรวมที่ลงทุนตราสารหนี้ (ต่อจากนี้เราจะเรียกค่าธรรมเนียมการจัดการ หรือ management fee แต่เพียงสั้น ๆ ว่า ค่าธรรมเนียม) เช่น อาจจะคิดค่าธรรมเนียมประมาณ 2 เปอร์เซ็นต์ สำหรับกองทุนรวมหุ้น และคิดค่าธรรมเนียมประมาณ 0.5 เปอร์เซ็นต์ สำหรับกองทุนรวมตราสารหนี้ เป็นต้น เพราะถือว่าการซื้อขายหุ้นจำเป็นต้องใช้ฝีไม้ลายมือและมีการวิเคราะห์ที่ซับซ้อนมากกว่า
หากคิดตามตรรกะนี้ กองทุนรวมประเภท 70/30 น่าจะคิดค่าธรรมเนียมถ่วงน้ำหนักไปตามสัดส่วนหุ้นที่ลงทุน เช่น (0.7 x 2.00) + (0.3 x 0.50) = 1.55 เปอร์เซ็นต์ สำหรับตัวอย่างข้างต้น และเราจะมาดูกันว่าในโลกความจริง ค่าธรรมเนียมของ บลจ. ต่าง ๆ เป็นไปตามนี้หรือไม่
(ต่อไปนี้เป็นข้อมูลจริงของ บลจ. สามแห่งที่เป็นบริษัทลูกของธนาคารพาณิชย์ และเนื่องจากเราไม่มีกองทุนรวม LTF ประเภทตราสารหนี้ จึงใช้ข้อมูลกองทุนรวมตราสารหนี้ RMF จาก บลจ. เดียวกันมาเทียบเคียงแทน ส่วนกองทุน "Homemade" ที่อยู่ขวาสุดเป็นกองทุนสมมติ)
พึงสังเกตว่าคอลัมน์สีชมพูด้านซ้ายเป็นค่าธรรมเนียมของกองทุนประเภท 70/30 ที่เรียกเก็บจริง ส่วนคอลัมน์สีชมพูด้านขวาเป็นค่าธรรมเนียมที่ “น่าจะ” เรียกเก็บ ซึ่งก็สรุปได้ว่าทุก บลจ. ที่เรายกมาเป็นตัวอย่างล้วนเก็บค่าธรรมเนียมจากกองทุนประเภท 70/30 แพงกว่าที่ควรด้วยกันทั้งสิ้น โดยส่วนต่างที่มากที่สุดเป็นของ บลจ. C ซึ่งเรียกเก็บสูงกว่าที่ควรถึง 1.61 – 1.29 = 0.32 เปอร์เซ็นต์ (แม้ที่จริง บลจ. C จะคิดค่าธรรมเนียมกองทุนหุ้นถูกที่สุดในบรรดาตัวอย่างที่ยกมา)
ในกรณีเช่นนี้ หากเราสามารถแยกเงินไปยังกองทุนหุ้นและกองทุนพันธบัตรด้วยตัวเองในสัดส่วน 70:30 ผลตอบแทนเฉลี่ยที่ได้รับจะใกล้เคียงกับการซื้อกองทุนประเภท 70/30 จาก บลจ. เดียวกัน แต่เสียค่าธรรมเนียมต่ำกว่า อย่างไรก็ดี เรา ไม่ สามารถทำสิ่งนี้ได้กับกองทุนรวม LTF เนื่องจากกฎเกณฑ์ที่ระบุให้ลงทุนหุ้นเฉลี่ยอย่างน้อย 65 เปอร์เซ็นต์ของสินทรัพย์กองทุน (ไม่เช่นนั้นเราก็จะต้องข้ามประเภทไปหา RMF ซึ่งจะมีกองทุนรวมตราสารหนี้ให้เลือกได้)
สถานการณ์ทั้งหมดนี้จะแตกต่างไปเมื่อลดหย่อนภาษีด้วย SSF หรือกองทุนรวมเพื่อการออม เพราะแม้เงื่อนไขหลาย ๆ อย่างอาจดูด้อยกว่า LTF แต่กองทุนรวม SSF ก็ไม่มีข้อจำกัดเรื่องสินทรัพย์
หากเราซื้อกองทุนรวม SSF เป็นจำนวนเงิน 200,000 บาท โดยแยกเงิน 70 เปอร์เซ็นต์ หรือ 140,000 บาท ไปยังกองทุนรวม SSF หุ้น และอีก 30 เปอร์เซ็นต์ หรือ 60,000 บาท ไปยังกองทุนรวม SSF ตราสารหนี้ เมื่อมองในภาพรวม เรากำลังลงทุนแบบ 70/30 แต่จ่ายค่าธรรมเนียมต่ำกว่าการซื้อกองทุนรวม SSF ประเภท 70/30 โดยตรง (ภายใต้สมมติฐานว่า บลจ. จะออกกองทุนรวม SSF ประเภทต่าง ๆ และคิดค่าธรรมเนียมในแนวทางเดียวกับ LTF/RMF)
เมื่อทำแบบนี้ เราจะสามารถประหยัดค่าธรรมเนียมได้ 0.32% ต่อปี เป็นเวลา 10 ปี ค่าธรรมเนียมที่ประหยัดได้จะคิดเป็นเงิน 6,400 บาท และถ้าใช้สิทธิ์ลดหย่อนทั้งห้าปีตามแนวทางเบื้องต้นของกระทรวงการคลัง (พ.ศ. 2563-2567) ค่าธรรมเนียมที่ประหยัดได้ทั้งสิ้นจะเท่ากับ 32,000 บาท ซึ่งก็ไม่น้อยเลย
นี่เป็นส่วนดีเล็ก ๆ อย่างหนึ่งจากเงื่อนไขของ SSF
วันพฤหัสบดีที่ 17 ตุลาคม พ.ศ. 2562
การต่อสู้ด้วยราคา
มีหนังสือและบทความมากมายบอกให้หลีกเลี่ยงหุ้นของบริษัทที่มีการแข่งขันกันอย่างดุเดือด โดยเฉพาะการ “แข่งกันลดราคา” ในที่นี้จะมาดูกันว่าทำไม
เราเคยกล่าวถึงในบทความที่แล้วว่า การเติบโตของกำไรสุทธิ (gNP) สามารถหาได้จาก การเติบโตของยอดขาย (gS) และ การเปลี่ยนแปลงของอัตรากำไรสุทธิ (ΔNPM / NPM0) ดังสมการ
โดยทั่วไปเมื่อบริษัทพยายามแข่งขันด้วยการลดราคาขาย ขณะที่สัดส่วนต้นทุนต่าง ๆ ยังคงเดิม อัตรากำไรสุทธิย่อมลดลง ส่งผลให้ (ΔNPM / NPM0) ติดลบ และอย่างน้อยที่สุดหากบริษัทต้องการรักษาระดับกำไรเอาไว้ให้ได้ (กำไรสุทธิมีการเติบโตเป็นศูนย์พอดี) บริษัทจะต้องพยายามทำให้ “ยอดขาย” มีการเติบโตมากพอ
ในกรณีดังกล่าว เราสามารถแทนค่า gNP = 0 เข้าไปในสมการ ทำให้ได้แผนภาพที่แสดงความสัมพันธ์ระหว่างตัวแปรสองตัวที่เหลือ
ตัวอย่าง
บมจ.ขนมไทยใจสู้ สามารถทำยอดขายในปีที่ผ่านมาได้ 100 ล้านบาท มีต้นทุนและค่าใช้จ่ายรวม 90 ล้านบาท บริษัทจึงมีกำไรสุทธิ 100 - 90 = 10 ล้านบาท คิดเป็นอัตรากำไรสุทธิ 10 เปอร์เซ็นต์ ในปีนี้บริษัทตัดสินใจลดราคาสินค้าลง 5 เปอร์เซ็นต์ เพื่อกระตุ้นยอดขาย (ใจสู้จริง ๆ)
ราคาสินค้าที่ปรับลง 5 เปอร์เซ็นต์ จะทำให้ยอดขายหดจาก 100 ล้านบาท เหลือ 95 ล้านบาท (ในขั้นแรกนี้เราจะยังไม่คิดเรื่องจำนวนชิ้นสินค้าที่จะขายได้เพิ่มขึ้น และตัดรายละเอียดเรื่องภาษีออกไป เพื่อลดความซับซ้อน) ภายใต้โครงสร้างต้นทุนเดิม กำไรสุทธิของบริษัทจะลดลงเหลือ 95 – 90 = 5 ล้านบาท คิดเป็นอัตรากำไรสุทธิ 5 / 95 = 5.3 เปอร์เซ็นต์
ในการนี้ ΔNPM / NPM0 จะเท่ากับ (0.053 – 0.10) / 0.10 = -0.47
หากดูจากแผนภาพ บริษัทจำเป็นต้องสร้างยอดขายที่เป็นจำนวนเงินให้เติบโตขึ้นราว 89 เปอร์เซ็นต์ หรือเพิ่มขึ้นเป็น 189 ล้านบาท จึงจะสามารถชดเชยกับอัตรากำไรสุทธิที่ลดลงได้ ซึ่งหากคิดเป็น “จำนวนชิ้น” สินค้าที่ต้องขาย จะคิดเป็นประมาณสองเท่า (189 / 95 = 2.0) ของปีล่าสุด
อย่างไรก็ตาม การจะลดราคาสินค้าเพียง 5 เปอร์เซ็นต์ แล้วหวังว่าจะขายของได้มากขึ้นเป็นเท่าตัวไม่ใช่เรื่องง่าย และที่สำคัญทั้งหมดนี้เพียงแค่จะรักษากำไรให้ได้ “เท่าเดิม” เท่านั้น
------------------------
สรุปก็คือ การลดราคาเพื่อกระตุ้นยอดขายนั้นมักจะให้ผลลัพธ์ที่ค่อนข้างแย่ โดยเฉพาะเมื่อบริษัทมีอัตรากำไรที่บางมาก และมีการประหยัดจากขนาด (economy of scale) มากพอตัวอยู่แล้ว
นอกจากนี้เมื่อบริษัทแห่งหนึ่งเริ่มลดราคา คู่แข่งก็มักหันมาลดราคาเพื่อรักษาฐานลูกค้าด้วย กลายเป็นว่าส่วนแบ่งตลาดของแต่ละรายคงเดิม แต่ยอดขายที่เป็นจำนวนเงินกลับลดลงกันถ้วนหน้า
เมื่ออัตรากำไรลด แถมยอดขายก็ยังหดอีก สองสิ่งนี้จะเสริมแรงกัน ทำให้กำไรสุทธิร่วงลงอย่างรุนแรง กอดคอกันไปพร้อมกับราคาหุ้น
นั่นเป็นเหตุผลที่ชัดเจนว่า เหตุใดเราจึงควรหลีกเลี่ยงบริษัทที่เน้นต่อสู้กันด้วยราคา ถ้าไม่อยากจะเสียใจในภายหลัง
วันอังคารที่ 8 ตุลาคม พ.ศ. 2562
การเติบโตของกำไร
ดูเหมือนแนวคิดที่บอกว่า “กำไร คือ เจ้ามือตัวจริงที่จะผลักดันราคาหุ้น” จะเริ่มเป็นที่แพร่หลายจากคำพูดของเซียนหุ้นวีไอ คุณโจ ลูกอีสาน (อนุรักษ์ บุญแสวง) อิทธิพลของแนวคิดนี้ทำให้ผู้เล่นในตลาดส่วนหนึ่งเปลี่ยนบทบาทจากนักเก็งกำไรที่พยายามคาดเดาทิศทางราคาหุ้น มาเป็นนักลงทุนที่พยายามคาดการณ์กำไรของบริษัทแทน
โดยธรรมชาติของการคาดการณ์ตัวเลข เรามักเริ่มต้นจากการดูข้อมูลย้อนหลัง ตัวอย่างเช่น ถ้าเราอยากรู้กำไรของปีหน้า เราก็อาจจะดูตัวเลขกำไรย้อนหลังไป 3-5 ปี เพื่อนำมาเป็นข้อมูลในการ “เก็ง” ตัวเลขของปีต่อไป ซึ่งดูเผิน ๆ ก็น่าจะเป็นความคิดที่ดี นอกเสียจากเราจะตระหนักถึงความจริงที่ว่า กำไรสุทธิ ของบริษัท เกิดจากการนำตัวเลขใหญ่ก้อนหนึ่ง (ยอดขาย หรือรายได้ของบริษัท) มาหักด้วยตัวเลขใหญ่อีกก้อนหนึ่ง (ต้นทุนและค่าใช้จ่ายต่าง ๆ) เมื่อการคำนวณเป็นดังนี้ กำไรสุทธิของบริษัทจึงมีความอ่อนไหวต่อการเปลี่ยนแปลง และการเติบโตของมันก็เป็นสิ่งที่คาดการณ์ได้ยาก
คาดการณ์โดยตรง
หลังจากผลประกอบการของปี 2017 ประกาศออกมา สมมติว่านักลงทุนท่านหนึ่งอยากคาดการณ์กำไรสุทธิของกิจการค้าปลีกแห่งหนึ่ง จึงเปิดหาข้อมูลจากเว็บไซต์ตลาดหลักทรัพย์ฯ ได้ดังนี้
รูปแบบที่ 1 นักลงทุนอาจสังเกตว่ากำไรสุทธิของปี 2016 เพิ่มขึ้นจากปีก่อนหน้าราว 3,000 ล้านบาท และต่อมาในปี 2017 กำไรสุทธิก็เพิ่มขึ้นอีกประมาณ 3,200 ล้านบาท ด้วยความที่เคยเรียนวิชาเลขอนุกรม นักลงทุนท่านนี้อาจเห็นความสัมพันธ์ของตัวเลขและคาดการณ์ว่ากำไรของปีต่อไปน่าจะเพิ่มขึ้นอีก 3,400 ล้านบาท... กลายเป็นกำไรสุทธิ 23,300 ล้านบาท ในปี 2018
รูปแบบที่ 2 นักลงทุนอาจคำนวณว่าอัตราการเติบโตของกำไรสุทธิปี 2016 เท่ากับ (16677 – 13682) / 13682 = 21.9% และอัตราการเติบโตของปี 2017 เท่ากับ (19908 – 16677) / 16677 = 19.4% นักลงทุนท่านนี้ตั้งข้อสังเกตว่าฐานกำไรที่ใหญ่ขึ้นของบริษัทอาจทำให้เปอร์เซ็นต์การเติบโตค่อย ๆ ลดลง เขาจึงคาดหวังการเติบโตในระดับ 18% สำหรับปีต่อไป หรือคิดเป็นกำไรสุทธิ 19908 x 1.18 = 23,491 ล้านบาท
คาดการณ์โดยอ้อม
นอกจากการคาดการณ์โดยตรงจากข้อมูลกำไรสุทธิแล้ว นักลงทุนยังสามารถคาดการณ์โดยอ้อมจากตัวเลขที่มีความมั่นคงมากกว่าอย่างยอดขายก็ได้
เริ่มต้นจากนิยามของ อัตรากำไรสุทธิ (Net Profit Margin: NPM) โดยนำ กำไรสุทธิ (Net Profit: NP) มาหารด้วย ยอดขาย (Sales: S)
* ในที่นี้อนุโลมให้ ยอดขาย = รายได้
แล้วก็ห้อย “ตัวเลขปี” กำกับไว้ด้วย เช่น NP1 เป็นกำไรสุทธิของปีที่ 1 ส่วน S1 ก็เป็นยอดขายของปีที่ 1 ฯลฯ สำหรับ ∆NPM ก็เป็นการเปลี่ยนแปลงของอัตรากำไรสุทธิ
เมื่อจับสมการข้างต้นมาหารกัน
ซึ่งถ้าย้อนไปที่นิยามของ “การเติบโต” ก็เกือบจบแล้ว
แทนค่าแบบซื่อ ๆ เข้าไปในสมการก่อนหน้านี้
สมการสุดท้ายนี้บอกเราว่า แทนที่จะประเมินการเติบโตของกำไรโดยตรง เราสามารถประเมินการเติบโตของรายได้หรือยอดขาย (gS) และคาดการณ์การเปลี่ยนแปลงของอัตรากำไรสุทธิ (∆NPM) ก็ใช้ได้เหมือนกัน
กลับไปที่ตัวอย่างการคาดการณ์กำไร
รูปแบบที่ 3 สมมติว่านักลงทุนท่านเดิมย้อนกลับไปที่ข้อมูลของบริษัทค้าปลีก
อัตราการเติบโตของรายได้ในปี 2016 เท่ากับ (451939 – 405893) / 405893 = 11.3% และการเติบโตของรายได้ในปี 2017 เท่ากับ (489403 – 451939) / 451939 = 8.3% ด้วยข้อสังเกตว่าฐานรายได้ที่ใหญ่ขึ้นของบริษัทอาจทำให้เปอร์เซ็นต์การเติบโตค่อย ๆ ลดลง นักลงทุนจึงคาดว่ารายได้จะมีการเติบโตในระดับ 7% สำหรับปีต่อไป
เนื่องจากบริษัทมีการปรับโครงสร้างเงินกู้ยืมในสองปีล่าสุด ส่งผลให้ภาระดอกเบี้ยจ่ายลดลง และสะท้อนออกมาด้วยอัตรากำไรสุทธิที่สูงขึ้น อย่างไรก็ตาม นักลงทุนประเมินว่าโครงสร้างเงินกู้ยืมดังกล่าวเริ่มเข้าที่เข้าทางแล้ว ประกอบกับความสามารถการทำกำไรที่ค่อนข้างอยู่ตัว จึงประเมินว่าอัตรากำไรสุทธิน่าจะคงเดิมที่ 4.07% (การเปลี่ยนแปลงเป็นศูนย์)
เมื่อผนวกมุมมองทั้งสองอย่างนี้เข้าด้วยกัน การเติบโตของกำไร (gNP) จะคำนวณตามสมการได้เท่ากับ 0.07 + (0 x 1.07) = 7% หรือเพิ่มขึ้นเป็น 19908 x 1.07 = 21,302 ล้านบาท ในปี 2018
สิ่งที่เกิดขึ้นจริง
ในเวลาต่อมาบริษัทประกาศผลการดำเนินงานของปี 2018 นักลงทุนพบว่าบริษัทมีกำไรจริงประมาณ 20,930 ล้านบาท หรือเพิ่มขึ้นราว 1,000 ล้านบาท คิดเป็นการเติบโตของกำไร 5.1%
หากย้อนกลับไปที่การคาดการณ์กำไรรูปแบบที่ 1 และรูปแบบที่ 2 ข้างต้น ตัวเลขที่เกิดขึ้นจริงนี้ควรถือว่า “ผิดคาด” ไปมาก แต่กับการคาดการณ์รูปแบบที่ 3 ตัวเลขนี้นับว่าใกล้เคียงทีเดียว
แน่นอน บางท่านอาจแย้งขึ้นมาว่า อันที่จริงเราสามารถใส่การวิเคราะห์เพิ่มเติมเข้าไปในการคาดการณ์สองรูปแบบแรกได้ด้วยเหมือนกัน อย่างเช่น ตัดผลกระทบของการประหยัดดอกเบี้ยจ่าย เพื่อหาอัตราการเติบโตที่มาจากการดำเนินงานล้วน ๆ นี่ก็อาจเป็นอีกหนึ่งวิธีที่ทำให้การคาดการณ์แม่นยำขึ้นได้
ข้อคิดที่อยากให้ไว้ คือ แม้ความสามารถในการวิเคราะห์ของเราจะมีเท่าเดิม แต่ความรู้ + วิธีคิดที่ดีและหลากหลายขึ้นอาจทำให้เราสามารถคาดการณ์ได้แม่นยำขึ้นก็ได้ และถ้า “กำไร คือ เจ้ามือตัวจริงที่จะผลักดันราคาหุ้น” แล้วล่ะก็ เมื่อคาดการณ์กำไรได้ดีขึ้นก็จะเท่ากับคาดการณ์ราคาหุ้นได้ดีขึ้นด้วย
วันพุธที่ 26 มิถุนายน พ.ศ. 2562
ห่วงเงินต้น... จนหมดตัว
ด้วยแนวคิดที่ว่า "เมื่ออายุมากขึ้น คนเราควรลงทุนอย่างอนุรักษนิยมมากขึ้น" พอร์ตลงทุนของคนวัยเกษียณจึงมักถูกออกแบบให้มีความระแวดระวัง โดยพยายามอย่างถึงที่สุดที่จะไม่ให้ขาดทุนหรือสูญเสียเงินต้นเลย แม้ได้ผลตอบแทนน้อยก็ไม่เป็นไร
การลงทุนอย่างระมัดระวังสุด ๆ โดยมุ่งรักษาเงินต้น อาจทำให้คนวัยทำงานรวยช้า แต่กับคนวัยเกษียณ นี่อาจทำให้หมดตัวได้ เหตุผลก็เพราะว่าโดยทั่วไปแล้วคนวัยเกษียณมักจำเป็นต้องดึงเงินบางส่วนออกมาจากพอร์ต เพื่อนำมาเป็นค่าใช้จ่ายในชีวิตประจำวัน (ต่างจากคนวัยทำงานที่มักใช้จ่ายเงินจากรายได้ประจำ แล้วส่วนที่เหลือเก็บจึงค่อยนำมาลงทุน)
เมื่อพอร์ตลงทุนให้ผลตอบแทนน้อยมาก เงินที่ดึงออกมาก็แทบจะเป็นส่วนของเงินต้นล้วน ๆ พอร์ตของเขาจึงหดลง เริ่มจากทีละน้อย และค่อย ๆ เร่งตัวมากขึ้นจนกระทั่งหมดไป
ตัวอย่างพอร์ตลงทุนของผู้เกษียณอายุที่มีค่าใช้จ่ายเดือนละ 20,000 บาท ภายใต้อัตราเงินเฟ้อ 3 เปอร์เซ็นต์ และได้ผลตอบแทน 1.87 เปอร์เซ็นต์ต่อปี เทียบเท่าผลตอบแทนจากพันธบัตรรัฐบาลที่มีอายุ 5 ปี
ทั้งนี้ เส้นตรงสีแดงในภาพกำกับไว้เพื่อให้เห็นชัดเจนขึ้นว่า การหดตัวลงของพอร์ตโฟลิโอมีการเร่งตัวในช่วงท้าย ก่อนที่มูลค่าพอร์ตจะกลายเป็นศูนย์ในระหว่างปีที่ 16 หลังเกษียณ ถ้าอายุเกษียณมาตรฐาน 60 ปี ก็เท่ากับว่ามีเงินใช้จ่ายถึงอายุ 75 ปีกว่า ๆ ใกล้เคียงกับอายุขัยเฉลี่ยของคนไทยตามข้อมูลจากธนาคารโลกพอดี ซึ่งสอดคล้องกับสื่อและแหล่งความรู้ทางการเงินที่แนะนำให้เก็บเงินเพื่อการเกษียณอย่างน้อย 4 ล้านบาท ตามที่เราเคยได้ยินกันมา
อย่างไรก็ตาม ท่านทั้งหลายควรตระหนักด้วยว่า การมีเงินแค่พอใช้ถึงค่าเฉลี่ยอายุขัยนั้นออกจะน่ากลัวเกินไป เพราะถ้าประเมินคร่าว ๆ ว่า ค่าเฉลี่ย อยู่ตรงประมาณกึ่งกลางของประชากรทั้งหมด โอกาสที่ตัวเราจะเป็นหนึ่งในประชากรที่มีอายุขัยยาวนานกว่าตัวเลขนี้ก็จะเท่ากับ 50-50 หรือพอ ๆ กับการโยนเหรียญ
จุดหมดตัว
ถึงตรงนี้หลายท่านน่าจะสังเกตเห็นความแตกต่างระหว่าง การลงทุน กับ การจัดการเงิน ของคนวัยเกษียณ ทั้งสองสิ่งนี้แม้จะมีความสัมพันธ์กัน แต่ก็เป็นคนละส่วนอยู่ดี
สำหรับชีวิตหลังเกษียณ ความมุ่งหมายสำคัญอยู่ที่การ "มีเงินใช้ตลอดชีพ" หาใช่การ "ไม่ขาดทุน" แต่อย่างใด ต่อให้เราลงทุนแล้วไม่เสียเงินเลย แต่การทยอยไถ่ถอนเงินทุนก็ทำให้หมดตัวได้ ณ จุดใดจุดหนึ่งในอนาคต ซึ่งผมขอเรียกว่า จุดหมดตัว ภารกิจของนักลงทุนวัยเกษียณ ได้แก่ การยืดจุดหมดตัวที่ว่านี้ให้ออกไปไกลที่สุด
เพื่อให้เห็นภาพชัดเจนขึ้น ลองมาดูตัวอย่างพอร์ตลงทุนที่แหล่งความรู้อื่น ๆ ไม่กล้าแนะนำกันบ้าง
นี่เป็นกรณีที่ค่อนข้างสุดขั้ว เมื่อคนวัยเกษียณนำเงินทั้งหมด 4 ล้านบาทเท่ากันไปลงทุนหุ้นและได้รับผลตอบแทนในระดับปานกลาง (หรืออาจจะค่อนข้างแย่เสียด้วยซ้ำในสายตาของบางท่าน) สังเกตว่า จุดหมดตัว ขยับไปอยู่ที่ปีที่ 29 หลังเกษียณ หรือเทียบเท่าอายุ 89 ปี
พอร์ตลงทุนแบบนี้นับว่า "เสี่ยงมากขึ้น" ในแง่ของการลงทุน เนื่องจากถือครองหุ้นเอาไว้เต็มอัตรา แต่ควรถือว่า "เสี่ยงน้อยลง" ในแง่ของการจัดการเงินในภาพรวม เพราะจุดหมดตัวอยู่ห่างออกไปมาก แม้จะยังคงกินอยู่และใช้จ่ายเท่าเดิม
ข้อสังเกตประการหนึ่งของพอร์ตสุดขั้วนี้ คือ ขนาดของพอร์ตมีการเติบโตขึ้นในช่วงแรก ก่อนจะลดลงในภายหลังด้วยอัตราเร่ง เหตุผลก็เพราะว่าผลตอบแทนรวมของพอร์ต 7 เปอร์เซ็นต์ เมื่อหักด้วยค่าใช้จ่ายปีละ 240,000 บาท ซึ่งคิดเป็น 6 เปอร์เซ็นต์ของมูลค่าพอร์ตตั้งต้น จะเท่ากับว่าขนาดของพอร์ตเติบโตได้เพียง 1 เปอร์เซ็นต์ต่อปี (ในช่วงแรก) ช้ากว่าค่าใช้จ่ายซึ่งเติบโตด้วยอัตราเงินเฟ้อ 3 เปอร์เซ็นต์ สุดท้ายจึงโดนค่าใช้จ่ายไล่กวดและต้องไถ่ถอนเงินต้นออกมามากขึ้นเรื่อย ๆ จนกระทั่งหมดตัวไปในที่สุด
หากต้องการมั่นใจว่าจะไม่หมดตัว ท่านจำเป็นต้องยืดจุดหมดตัวออกไปที่อินฟินิตี้ (infinity - ไม่มีที่สิ้นสุด) พูดง่าย ๆ ก็คือ สามารถมีกินมีใช้ตลอดชีวิต เหมือนที่เคยอธิบายไปในบทความชื่อ "แทะเงินก้อน" ซึ่งเหตุการณ์นี้จะเกิดขึ้นได้ ผลตอบแทนรวมของพอร์ตจะต้องเพิ่มขึ้นจาก 7 เปอร์เซ็นต์ เป็น 9 เปอร์เซ็นต์ สอดคล้องกับ สมการอิสรภาพทางการเงิน ที่เคยนำเสนอไปเมื่อ 6-7 ปีที่แล้ว
[ท่านทั้งหลายอาจอัศจรรย์ใจนิดหน่อย เมื่อองค์ความรู้ที่ค้นพบต่างกรรมต่างวาระ สุดท้ายก็กลับมาสอดคล้องกันเองราวกับจิ๊กซอว์ที่อยู่ในชุดเดียวกัน]
จัดพอร์ตให้เหมาะสม
ในกรณีที่ไม่สามารถยืด จุดหมดตัว ออกไปที่อินฟินิตี้ ท่านจำต้องยอมรับความจริงและจัดพอร์ตลงทุนให้เหมาะสม แน่นอนว่าท่านไม่ควรเอาเงินไปฝากธนาคารหรือซื้อกองทุนตราสารหนี้จนหมด ขณะเดียวกันการจัดพอร์ตสุดขั้วโดยลงทุนหุ้น 100 เปอร์เซ็นต์เหมือนในตัวอย่างข้างต้นก็ไม่น่าจะเป็นความคิดที่ดีนัก
ลองมาพิจารณาภาพด้านล่างนี้กัน
หากแบ่งช่วงเวลาหลังเกษียณออกเป็นช่วง ๆ ด้วยสูตรจำนวนปี "ยกกำลังสอง" เหมือนในรูป เราอาจประเมินว่าช่วงเวลาที่ใกล้จะมาถึง (เช่น 2 ปีแรก) เป็นช่วงที่ควรเตรียมเงินสดพร้อมใช้ รูปแบบของสินทรัพย์ที่เหมาะสมกับเงินก้อนนี้ ได้แก่ เงินฝากธนาคาร หรือกองทุนตราสารเงิน ซึ่งสามารถไถ่ถอนได้ภายใน 1-2 วัน โดยไม่ลดมูลค่า
เงินก้อนสำหรับช่วงเวลา 4 ปีถัดไป (เช่น ปีที่ 2 ถึงปีที่ 6) สามารถเลือกลงทุนในสินทรัพย์ที่สร้างผลตอบแทนสูงขึ้นและมีความผันผวนไม่มาก เช่น กองทุนตราสารหนี้ระยะสั้นหรือระยะกลาง ส่วนสินทรัพย์ที่เหมาะสำหรับค่าใช้จ่ายในช่วงปีที่ 6 ถึงปีที่ 14 อาจเน้นไปที่การสร้างกระแสเงินสดและการเติบโตมากขึ้น เช่น กองทุนรวมที่กระจายลงทุนในกองรีท (REIT) หรือกองทุนรวมอสังหาริมทรัพย์หลาย ๆ กอง หรือแม้แต่กองทุนรวมหุ้นที่เน้นหุ้นปันผลดี
ในส่วนของสินทรัพย์ที่จะรองรับค่าใช้จ่ายช่วงปีที่ 14 ถึงปีที่ 30 เราน่าจะสามารถสร้างผลตอบแทนและเอาชนะเงินเฟ้อได้ด้วยการลงทุนหุ้นอย่างเต็มที่ เนื่องจากเป็นการลงทุนระยะยาวและกว่าจะต้องใช้เงินก้อนนี้ก็ยังอีก 14 ปีข้างหน้า หากเศรษฐกิจเกิดชะงักงัน อย่างน้อยก็มีเวลานับทศวรรษให้ตลาดหุ้นฟื้นตัว สิ่งสำคัญก็คือ อย่าลืมกระจายการลงทุนไปในหุ้นหลาย ๆ ตัว เพราะ "ตลาดหุ้น" ในภาพรวมมักฟื้นได้หลังวิกฤติ แต่กับ "หุ้นหนึ่งตัว" นั้นไม่แน่
เมื่อพิจารณาดังนี้แล้ว สมมติว่าเรามีเงินเกษียณ 4 ล้านบาท และเตรียมค่าใช้จ่ายไว้ปีละ 240,000 บาท เงินสำหรับสองปีแรกจะเท่ากับ 240000 x 2 = 480,000 บาท ตีง่าย ๆ ว่าก้อนนี้เอาไปฝากธนาคาร
[เพื่อไม่ให้ซับซ้อนมากนัก เราจะตัดเรื่องเงินเฟ้อออกไป แต่ท่านทั้งหลายไม่ต้องกังวล เพราะการลงทุนในภาพรวมของเราให้ผลตอบแทนที่น่าจะพอสู้กับเงินเฟ้อได้อยู่แล้ว]
เงินสำหรับสี่ปีถัดมา 240000 x 4 = 960,000 บาท เอาไปซื้อกองทุนรวมตราสารหนี้
เงินสำหรับแปดปีต่อไป 240000 x 8 = 1,920,000 บาท เอาไปซื้อกองทุนรวมที่ลงทุนในกองอสังหาฯ และกองทุนรวมที่เน้นหุ้นปันผลดี อย่างละเท่า ๆ กัน
เงินส่วนที่เหลือจะเท่ากับ 4000000 - 480000 - 960000 - 1920000 = 640,000 บาท ส่วนนี้เป็นเงินที่เตรียมไว้ใช้จ่ายตั้งแต่ปีที่ 14 เป็นต้นไป จึงเอาไปซื้อกองทุนหุ้น
สรุปตัวอย่างพอร์ตตั้งต้น
*** ข้อสรุปนี้เกิดจากตัวเลขและสมมติฐานข้างต้น เพื่อประโยชน์ในการนำเสนอแนวคิดเท่านั้น ***
นี่เป็นตัวอย่างการจัดพอร์ตลงทุนให้สอดคล้องกับระยะเวลาที่เหลืออยู่ของชีวิตคนวัยเกษียณ ซึ่งมีข้อสังเกตอยู่ 3-4 ประการ
ประการแรก พอร์ตดังกล่าวนี้เป็นเพียง "พอร์ตตั้งต้น" ซึ่งแน่นอนว่าเมื่อเวลาผ่านไป เราก็จะต้องปรับส่วนผสมในพอร์ตเป็นระยะ โดยอาจย้อนกลับไปยังแถบสีที่แบ่งช่วงปีอีกครั้งหนึ่ง แล้วแบ่งสรรสินทรัพย์ไปตามหมวดหมู่เสียใหม่ทุกปีหรือทุกสองปี
ประการที่สอง พอร์ตลงทุนนี้มี จุดหมดตัว ณ ต้นปีที่ 19 หลังเกษียณ เทียบกับกรณีลงทุนอย่างระมัดระวังสุด ๆ [ภาพแรกของบทความ] ซึ่งมีจุดหมดตัวอยู่ประมาณกลางปีที่ 16 การยืดจุดหมดตัวออกไปได้เกือบสามปีนับว่ามีคุณค่าอย่างยิ่งสำหรับคนวัยเกษียณที่กำลังหลังพิงฝา
ประการที่สาม ท่านสามารถใช้แถบสีจำนวนปีรูปแบบอื่น เช่น แทนที่จะกำหนดช่วงแบบยกกำลังสอง (2-4-8-16 ปี) ท่านอาจใช้ตัวเลขง่าย ๆ อย่างเช่น 5-10-15 ปี ก็ได้ โดยหลักแล้วเราจะไม่มีปัญหากับตัวเลขที่แตกต่างกัน ตราบเท่าที่มันสะท้อนแนวคิดเรื่องการลงทุนระยะสั้น-ระยะยาว
ประการที่สี่ สัดส่วนการถือครองหุ้นในระดับ 40 เปอร์เซ็นต์ อาจทำให้กูรูหลายท่านไม่พอใจนัก เพราะพวกเขาคุ้นเคยและมักให้คำแนะนำประเภทบอกต่อกันมา เช่น "คนวัยเกษียณควรถือครองหุ้น 5 เปอร์เซ็นต์ และถือตราสารหนี้กับเงินฝากธนาคารในสัดส่วนที่มาก" แบบนี้ท่านควรถามเขาด้วยว่า "ตัวเลข 5 เปอร์เซ็นต์มาจากไหน?" บางทีท่านอาจจะประหลาดใจที่แม้แต่กูรูเองก็คอนเฟิร์มคำแนะนำของตัวเองไม่ได้ และอาจหงุดหงิดกับคำถามของท่านด้วยซ้ำไป
ส่วนพอร์ตตัวอย่างของเรา เราได้เห็นกันแล้วว่าตัวเลข 40 เปอร์เซ็นต์ มีที่มาอย่างไร และถ้าท่านใส่สมมติฐานใหม่ตามสถานการณ์ของตนเองเข้าไปในโมเดล ตัวเลขใหม่ที่ได้ก็จะถือว่ามีที่มาเช่นกัน ซึ่งท่านสามารถมั่นใจได้มากกว่าคำแนะนำแบบกำปั้นทุบดินที่ฟังต่อกันมา นอกจากนั้นพอเวลาผ่านไป สัดส่วนการลงทุนหุ้นจะลดลงจนเหลือศูนย์ไปเอง หากมีการปรับพอร์ตอย่างสม่ำเสมอตามที่บอกไปข้างต้น นี่เป็นกลไกที่เกิดขึ้นเพื่อผสานแนวคิดเรื่อง การลงทุน และ การจัดการเงิน เข้าด้วยกัน
สำหรับประเด็นเรื่องความเสี่ยงและสัดส่วนการถือครองหุ้นนี้ ไว้ผมจะพยายามหาโอกาสอธิบายเพิ่มเติมในแฟนเพจเฟซบุ๊ก MonkeyFreeTime ต่อไป
วันพุธที่ 12 มิถุนายน พ.ศ. 2562
แทะเงินก้อน
เป็นที่เชื่อกันโดยทั่วไปว่าเราจำเป็นต้องมีเงินก้อนใหญ่ เพื่อเอาไว้แทะกินหลังเกษียณ บางกระแสระบุว่าจำนวนเงินขั้นต่ำ คือ 4 ล้านบาท แต่ถ้าอยากให้ชีวิตมีคุณภาพ ก็อาจต้องมีถึง 10 ล้านบาท โดย “ดีไซน์” ของการเกษียณในรูปแบบนี้อยู่ตรงที่การทยอยใช้เงินก้อนดังกล่าว และหวังว่าจะไม่หมดเงินก่อนหมดลม
เคยได้ยินไหมครับ ที่เขาบอกว่า “สุดเสียดาย ตายไปยังใช้เงินไม่หมด” กับ “สุดสลด ใช้เงินจนหมดแล้วยังไม่ตาย”
คำถามที่เกิดขึ้นในใจของผม คือ ชีวิตของเราควรจะลุ้นขนาดนั้นเชียวหรือ? และหากมีถึง 10 ล้านบาทจริง เรายังจำเป็นต้องนั่งแทะเงินด้วยใจตุ๊ม ๆ ต่อม ๆ อีกไหม หรือที่จริงเราสามารถเอาเงินก้อนที่ว่ามาสร้างกระแสเงินสดไว้เลี้ยงตัวได้ตลอดชีพสบาย ๆ... และจุดแบ่ง (ว่าจะแทะหรือไม่แทะ) มันอยู่ตรงไหน?
โมเดลการเลี้ยงชีพ
เพื่อตอบคำถามข้างต้น ผมได้สร้างโมเดลที่จะค้นหาความจริง โดยกำหนดให้ชาวเกษียณมีรายได้สองทาง ได้แก่
- กระแสเงินสดที่ไม่ต้องออกแรงทำงาน (Passive Cash Flow หรือ P) และ
- เงินที่ทยอยไถ่ถอนมาจากเงินก้อน (Cash Redemption หรือ R)
เมื่อนำรายได้ข้างต้นหัก ค่าใช้จ่าย (Expense หรือ X) เรียบร้อยแล้ว หากมีเงินสดเหลือ เราจะเรียกว่า Cash Leftover หรือ L ซึ่งทั้งหมดจะสามารถเขียนเป็นสมการการใช้เงินของชาวเกษียณในปีที่ 1 ได้ดังนี้
สังเกตว่าในสมการ เราคำนึงถึงเงินสดที่เหลือมาจากปีก่อนหน้า (ปีที่ศูนย์) หรือ L0 ด้วย
จากแนวคิดนี้ เราสามารถเขียนสมการให้อยู่ใน รูปทั่วไป ก็ได้ โดยตัวเลข 1 ที่ห้อยไว้เพื่อแสดงว่าเป็นปีที่ 1 ก็จะเปลี่ยนเป็น i และท่านก็จะสามารถแทนค่า i ให้เป็นตัวเลขปีใด ๆ ที่ท่านต้องการ
เมื่อย้ายข้างจัดรูปเสียหน่อยก็จะได้
หากสังเกตให้ดี ฝั่งขวาของสมการเป็นกระแสเงินสดที่ไหลเข้าและไหลออกในปีนั้น ๆ ส่วนฝั่งซ้ายก็เป็นการสรุปว่าเงินสดที่คงค้างอยู่ในระบบมีการเปลี่ยนแปลงไปเท่าไร
ภาพรวมหลังเกษียณ
แน่นอนว่าความสนใจของเรา ไม่ใช่ ชีวิตหลังเกษียณปีใดปีหนึ่ง แต่เป็นภาพรวมของทุก ๆ ปีภายหลังเกษียณ สมมติว่าเรามีชีวิตอยู่ต่อไปหลังเกษียณแล้วอีก n ปี (ถ้าท่านเกษียณที่อายุ 60 ปี และมีชีวิตอยู่ต่อได้อีก n = 25 ปี นั่นหมายความว่า ท่านคาดการณ์อายุขัยของตนเองไว้เท่ากับ 60 + 25 = 85 ปี) เพื่อให้ครอบคลุมความสนใจของเรา เราก็จะคำนวณ “ผลบวก” ของทุกปี ตั้งแต่ปีที่ 1 ไปจนถึงปีที่ 25 นั่นเอง
[สำหรับท่านที่ไม่คุ้นเคย ซิกมา หรือ Σ เป็นตัวอักษรกรีกที่แปลเป็นภาษาคนง่าย ๆ ว่า “ผลบวก”]
เมื่อคิดผลบวก (ตั้งแต่ปีที่ 1 จนถึงปีที่ n) กับทั้งสองฝั่งของสมการ จะได้
หากลองแทนค่า i = 1, 2, 3,... ไปจนถึง n จะพบว่าฝั่งซ้ายของสมการเท่ากับ Ln – L0 ซึ่งเราออกแบบให้มีการไถ่ถอนหรือสร้างกระแสเงินให้พอดีกับที่จะใช้จ่าย ทำให้ไม่มีการสะสมเงินสดคงค้าง และฝั่งซ้ายนี้ก็จะกลายเป็นศูนย์ ส่วนฝั่งขวาของสมการนั้น พจน์ที่หนึ่ง (ΣP) และพจน์ที่สาม (ΣX) สามารถลดรูปลงได้
จากสมมติฐานที่ว่า Passive Cash Flow ในแต่ละปีมาจาก เงินปันผล ที่สินทรัพย์ A จ่ายออกมาด้วยอัตราผลตอบแทนเงินปันผล (d) ที่ค่อนข้างคงที่ ดังนั้น ΣP = Σ(dA) = d Σ(A) ในกรณีที่สินทรัพย์เป็นพอร์ตโฟลิโอที่ประกอบด้วยหุ้นของบริษัทที่มีธุรกิจอิ่มตัวและจ่ายเงินปันผลอย่างสม่ำเสมอ เราสามารถคาดการณ์การเติบโตในระยะยาวเท่ากับอัตราเงินเฟ้อ ส่วนค่าใช้จ่าย X ก็เติบโตในอัตราเดียวกับอัตราเงินเฟ้อด้วยเช่นกัน
เมื่อเป็นเช่นนี้ จะได้ว่า ΣA = nA1 และ ΣX = nX1 ทำให้สามารถเขียนสมการข้างต้นให้อยู่ในรูป real term ซึ่งตัดผลกระทบจากเงินเฟ้อออกไปได้
ดังนั้น เราจะต้องไถ่ถอนเงินสด (แทะเงินก้อน) ตลอดช่วงเวลาการเกษียณ เท่ากับ
ถ้า X1 = dA1 ฝั่งขวาของสมการจะกลายเป็นศูนย์ หมายความว่า เราไม่ต้องแทะเงินก้อนเลย และในทางตรงข้าม หากเราไม่มีสินทรัพย์ที่สร้างกระแสเงินสดเลย (A1 = 0) ก็จะได้ว่า ΣR = nX1 ซึ่งก็แปลว่า เราต้องเตรียมเงินก้อนเอาไว้เท่ากับค่าใช้จ่ายของปีแรก (X1) คูณด้วยจำนวนปีที่จะอยู่หลังเกษียณ (n) แล้วก็ต้องเอาไปฝากหรือทำอะไรให้มีผลตอบแทนเท่า ๆ กับอัตราเงินเฟ้อด้วย ถึงจะมีเงินพอให้แทะตลอดอายุขัย
การตัดสินใจครั้งสำคัญ
หากท่านต้องเลือกระหว่าง (1) การสร้างพอร์ตลงทุน A1 ที่สร้างกระแสเงินสดเลี้ยงเราไปตลอดชีพ และ (2) การเตรียมเงินก้อน ΣR ที่เพียงพอสำหรับการแทะกินไปได้ตลอดชีวิต นั่นแสดงว่าท่านกำลังเปรียบเทียบระหว่าง X1/d (เพราะว่า X1 = dA1) กับ nX1
ในกรณีที่ท่านสามารถสร้างพอร์ตลงทุนที่ให้ผลตอบแทนเงินปันผล d ที่มีค่ามากกว่า 1/n ได้ การสร้างกระแสเงินสดจะดีกว่าการแทะเงินก้อน
ตัวอย่างเช่น สมมติท่านเตรียมเกษียณที่อายุ 60 ปี และคาดว่าจะมีชีวิตอยู่ต่อไปหลังจากนั้น 25 ปี (n = 25) ด้วยการใช้จ่ายเดือนละ 2 หมื่นบาท การแทะเงินก้อนจะทำให้เงินเก็บ 6 ล้านบาทของท่านหมดไปพอดี เพราะ nX1 = 25 ปี x (20000 บาท x 12 เดือน) = 6,000,000 บาท
ในทางตรงข้าม หากท่านนำเงินจำนวนเดียวกันไปสร้างพอร์ตลงทุนที่ให้ผลตอบแทน d = 1/25 หรือ 4% ต่อปี พอร์ตลงทุนของท่านจะจ่ายเงินปันผลออกมาปีละ 0.04 x 6000000 = 240,000 บาท หรือเทียบเท่าเดือนละ 20,000 บาทพอดีเช่นกัน และเงินปันผลนี้ยังเติบโตเท่ากับอัตราเงินเฟ้อ (สมมติว่า 2 เปอร์เซ็นต์) ทำให้สามารถรองรับค่าใช้จ่าย (ซึ่งก็เพิ่มขึ้นในอัตราเดียวกับเงินเฟ้อด้วยเหมือนกัน) ได้ไปจนตลอดชีวิต
ความแตกต่างก็คือ เมื่อครบเวลา 25 ปีแล้ว การแทะเงินก้อนจะทำให้เงินเก็บ 6 ล้านบาทหมดสิ้นไป แต่พอร์ตลงทุนที่สร้างกระแสเงินสด นอกจากไม่หมดแล้วยังสามารถเติบโตขึ้นเป็น 6000000 x 1.02^25 = 9.84 ล้านบาทได้อีกต่างหาก ถ้าไม่ยกให้ลูกหลานญาติมิตร จะเขียนพินัยกรรมทำบุญส่งท้ายก็เป็นกุศลดี
ความเสี่ยงล่ะ?
ถึงตรงนี้หลายท่านคงเห็นแล้วว่าการสร้างกระแสเงินสดมีความยั่งยืนกว่าการแทะเงินก้อน แต่ก็อาจมีบางท่านกังวลในเรื่องของความเสี่ยง และคิดว่าอย่างน้อยถ้าเก็บเงินก้อนไว้แทะ เงินนั้นก็ยัง "ไม่หาย" จนกว่าเราจะหยิบมันออกมาใช้จ่าย ต่างจากพอร์ตลงทุนซึ่งอาจเจ๊งหมดตัวได้
ความกังวลข้อนี้มีทั้งที่จริงและไม่จริง ประการแรก คือ เงินก้อนที่เก็บไว้แทะก็อาจหายหรือลดน้อยลงได้เหมือนกัน แม้จะเป็นการซื้อกองทุนรวมตราสารหนี้ที่คิดว่ามีความเสี่ยงต่ำ เพราะผู้จัดการกองทุนอาจนำเงินของเราไปซื้อตราสารหนี้เอกชน ซึ่งก็มีความเสี่ยงที่จะผิดนัดชำระหนี้และทำให้เงินต้นหายไปได้ ตัวอย่างนี้มีให้เห็นมาแล้วในช่วงวิกฤติเศรษฐกิจของไทยเราเอง
ตัวอย่างผลขาดทุนจากกองทุนรวมตราสารหนี้ในช่วงวิกฤติเศรษฐกิจ
* ในช่วงเวลาดังกล่าว หลาย ๆ กองทุนประเภทเดียวกันก็มีชะตากรรมแบบนี้ นักลงทุนโปรดเข้าใจว่าเป็นความเสี่ยงตามประเภทของกองทุน *
ไม่เพียงเท่านั้น ในช่วงวิกฤติแม้แต่ธนาคารยังแทบเอาตัวกันไม่รอด เงินฝากธนาคารที่คิดว่าแน่ก็ยังอาจไม่แน่ได้เหมือนกัน หรือถ้าจะได้เงินคืนเต็มจำนวนก็อาจต้องใช้เวลามากขึ้น ส่วนผลตอบแทนก็แทบไม่ต้องพูดถึง
ประการที่สอง พอร์ตลงทุนอาจเจ๊งหมดตัวหรือไม่ก็ได้ ขึ้นอยู่กับ "ไส้ใน" ที่เราจัดไว้ หากพอร์ตลงทุนของเราประกอบด้วยหุ้นหวือหวาเก็งกำไร หุ้นที่มี P/E สูง ๆ เช่น 50-60 เท่า โอกาสที่ราคาหุ้นในพอร์ตจะปรับตัวลงแรง ๆ ก็เป็นไปได้มาก
ในทางกลับกัน หากท่านจัดพอร์ตให้มีหุ้นชั้นนำขนาดใหญ่ที่ผ่านร้อนผ่านหนาวและจ่ายเงินปันผลได้อย่างสม่ำเสมอมาเป็นสิบปี ผสมผสานกับกองทุนอสังหาริมทรัพย์และกองทุนตราสารหนี้ โอกาสที่ท่านจะเจ๊งหรือขาดทุนแรง ๆ ก็มีไม่มาก โดยเฉพาะเมื่อเป็นการลงทุนระยะยาว 20-30 ปี
ประการที่สาม แม้ท่านจะเห็น มูลค่าพอร์ต ลดลงหรือเพิ่มขึ้นตามสภาพตลาด แต่ตราบเท่าที่ "กระแสเงินสด" ยังแข็งแกร่ง ท่านก็ไม่มีเหตุให้วิตก เพราะสิ่งที่ท่านต้องการจริง ๆ คือ กระแสเงินสด ไม่ใช่มูลค่าพอร์ตครับ
วันเสาร์ที่ 9 กุมภาพันธ์ พ.ศ. 2562
วิจัยฝุ่น (PM 2.5) ภาษาชาวบ้าน
ในสถานการณ์ที่คนกรุงเทพฯ ต้องรับมือกับฝุ่นละอองขนาดจิ๋วที่รู้จักกันในนาม PM 2.5 จะมีอะไรดีไปกว่าการศึกษาเรื่องราวของมัน และเปลี่ยนภาษาต่างดาวจากบทความทางวิชาการ มาเป็นภาษาง่าย ๆ อย่างที่ชาวบ้านเข้าใจได้
ฝุ่นละอองขนาดเล็ก (Particulate Matter) หรือ PM นั้น รัฐบาลของชาติตะวันตกเขามีประสบการณ์และให้ความสำคัญมานานแล้ว อย่างไรก็ตาม ประเทศที่สร้างผลงานวิจัยอย่างจริงจังในระยะหลังกลับกลายเป็นจีน ซึ่งมีประสบการณ์ตรงเกี่ยวกับเรื่องนี้เยอะ โดยงานวิจัยมีทั้งที่เกี่ยวข้องกับ PM 2.5 และ PM 10 (ตัวเลขที่พ่วงมา หมายถึง ขนาดของฝุ่น ซึ่งวัดกันเป็น ไมครอน) รวมถึงสารพิษอื่น ๆ อีกหลายตัว แต่ในที่นี้เราจะหยิบมาเฉพาะที่กล่าวถึง PM 2.5 [รายชื่อเอกสารอ้างอิงมีอยู่ที่ท้ายบทความ]
ไปไงมาไง?
สิ่งที่ผู้คนทั่วไปมักจะสงสัย คือ ฝุ่นนี้มันมาจากไหน? แล้วจริง ๆ มันมีทุกปีหรือเปล่า ทำไมปีนี้สถานการณ์จึงหนักหนากว่าที่ผ่านมา
ก่อนอื่นต้องทำความเข้าใจว่า PM 2.5 ที่อยู่ในอากาศเป็นฝุ่นที่รวมกันมาจากสองส่วน ส่วนแรกเป็นฝุ่นมลพิษที่เกิดขึ้นจากภายในพื้นที่เอง และส่วนที่สองเป็นฝุ่นมลพิษ “ขาประจำ” ที่ล่องลอยในเขตภูมิภาคของเราอยู่แล้ว ดังนั้น หากเราหยุดกิจกรรมต่าง ๆ ที่ปล่อยฝุ่นมลพิษในพื้นที่จนหมดเกลี้ยง (สมมติว่าทำได้) เราก็จะกำจัดเฉพาะ ฝุ่นจากในพื้นที่ แต่เพียงเท่านั้น ส่วน ฝุ่นภูมิภาค จะยังคงมีอยู่ต่อไปตามธรรมชาติ การจำแนกฝุ่นสองส่วนนี้ออกจากกันจะทำให้เราทราบว่า ฝุ่นที่เราสามารถบริหารจัดการได้มีปริมาณเท่าใด เมื่อเทียบกับทั้งหมดที่วัดได้
ประเด็นสำคัญ #1: การจำแนก ฝุ่นจากในพื้นที่ กับ ฝุ่นภูมิภาค
ในความคิดของคนทั่วไป แหล่งที่มาสำคัญของฝุ่น PM 2.5 มาจากการยานพาหนะ โรงงานอุตสาหกรรม และการเผาในที่โล่งแจ้ง แต่นั่นก็ถือว่าถูกต้องเพียงครึ่งเดียว เพราะที่จริงแล้วฝุ่นมลพิษยังสามารถเกิดขึ้นจากกระบวนการทางเคมีในอากาศ ทำให้เกิดอนุภาคใหม่ขึ้นมาร่วมผสมโรงได้ด้วย
จากรายงานทางวิชาการที่สำรวจปริมาณฝุ่นในเมืองเทียนจิน ซึ่งตั้งอยู่ใกล้ ๆ กับกรุงปักกิ่ง ประเทศจีน พบว่าปริมาณฝุ่น PM 2.5 มาจากยานพาหนะ 16%, จากการก่อสร้างและฝุ่นเมือง 30%, จากถ่านหิน 20% และเป็นฝุ่นจากกระบวนการเคมี 28% ส่วนปริมาณฝุ่นในเมืองหนิงโป ซึ่งอยู่ใกล้กับเมืองเซี่ยงไฮ้ มีสัดส่วนจากยานพาหนะ 15%, จากฝุ่นเมือง 20%, จากถ่านหิน 14% และเป็นฝุ่นจากกระบวนการเคมี 36%
เราคงไม่สามารถสรุปได้ว่า สัดส่วนตามแหล่งที่มาของฝุ่น PM 2.5 ในกรุงเทพฯ จะใกล้เคียงกับทั้งสองเมืองนี้มากน้อยเพียงใด จนกว่าจะได้ทำการตรวจวัดอย่างถูกต้องตามหลักวิชาการ (ไม่ใช่แค่การประมาณตัวเลข แถมยังเป็นตัวเลขทั่วประเทศ) แต่สิ่งหนึ่งที่ผมอยากชี้ให้เห็น คือ ถ้ากรุงเทพฯ ของเรามีฝุ่นจากยานพาหนะอยู่ในระดับ 15-16 เปอร์เซ็นต์ เหมือนอย่างสองเมืองข้างต้นนั้น แม้จะเข้มงวดและลดควันพิษจากรถยนต์ลงได้ถึง 20 เปอร์เซ็นต์ แต่ผลกระทบในภาพรวมจะมีเพียง 0.20 x 15% = 3% เท่านั้น เราจึงต้องสืบเสาะหาแหล่งที่มาอื่น ๆ ของฝุ่น เพื่อกระทำทุกวิถีทางให้ผลรวมของฝุ่นลดลง ในทางกลับกัน หากเราไม่สำรวจแหล่งที่มาของฝุ่นให้เข้าใจ เราก็จะสาละวนอยู่กับควันรถยนต์ แล้วก็สงสัยว่าทำไมฝุ่นจึงไม่ลดลงเสียที
ประเด็นสำคัญ #2: การจำแนกแหล่งที่มาของฝุ่น
รู้หรือไม่
- ฝุ่น PM 2.5 สามารถปลิวไปได้ไกลหลายพันกิโลเมตรนับจากแหล่งกำเนิด
- มีการค้นพบว่าฝุ่น PM 2.5 ราว 40 เปอร์เซ็นต์ของที่วัดค่าได้ เป็นส่วนที่ลอยข้ามมาจากภูมิภาคอื่น (ดังนั้น มาตรการต่าง ๆ ที่เกิดขึ้นในเขตพื้นที่ ก็จะช่วยได้เฉพาะ 60 เปอร์เซ็นต์ที่เหลือ)
- ช่วงเวลาและระดับความสูง (เช่น กรณีอยู่อาศัยในตึกสูง) มีผลต่อปริมาณฝุ่น สังเกตได้จากตัวอย่างเมืองเทียนจินในสองรูปต่อไปนี้
- รูปแรก ที่ระดับความสูง 40 เมตร และระดับพื้นดิน ช่วงเวลาที่น่าสนใจ คือ 6.00-9.00 น. ปริมาณฝุ่นพุ่งขึ้นจากช่วงกลางคืนอย่างเห็นได้ชัด แต่เมื่อพ้น 10.00 น. ปริมาณฝุ่นกลับลดลงอย่างมาก และต่ำที่สุดในช่วง 15.00-16.00 น. ก่อนจะกลับมาคงตัวในช่วงหัวค่ำ
- ข้อสังเกตจากเรื่องนี้ คือ พวกเราออกจากบ้านแต่เช้าไปสูดฝุ่นในช่วงที่ปริมาณฝุ่นสูงสุดพอดี หากเราสามารถขยับเวลาเริ่มงานเป็นการชั่วคราวในช่วงที่มีวิกฤติฝุ่นครั้งต่อไป ก็จะลดผลกระทบต่อสุขภาพได้มาก
- รูปที่สอง ที่ระดับความสูง 220 เมตร (เทียบเท่าตึก 73 ชั้น) ปริมาณฝุ่นเริ่มพุ่งขึ้นในช่วง 9.00 น. ซึ่งช้ากว่าฝุ่นที่ระดับพื้นดิน จากนั้นค่อย ๆ ลดลงมาสู่ระดับปกติในช่วง 14.00 น. และช่วงค่ำปริมาณฝุ่นจึงค่อยลดลงต่ำสุด
- ข้อสังเกต คือ นอกเหนือจากรูปแบบ (โปรไฟล์) ที่แตกต่างกันแล้ว ปริมาณฝุ่นที่ระดับความสูงมาก ๆ โดยเฉลี่ยจะต่ำกว่าปริมาณฝุ่นที่ระดับพื้นดินอย่างชัดเจน แต่ถ้าเป็นความสูงเพียง 40 เมตร (เทียบเท่าตึก 13 ชั้น) ปริมาณฝุ่นจะพอ ๆ กับที่ระดับพื้นดิน
- จากข้อสังเกตดังกล่าว เราอาจอนุมานได้ว่า ฝุ่นจากในพื้นที่ น่าจะเป็นองค์ประกอบเด่นที่ระดับพื้นดิน และเมื่อสูงขึ้นไปมาก ๆ เช่น 220 เมตร ฝุ่นจากในพื้นที่น่าจะมีสัดส่วนลดลง และทำให้ ฝุ่นภูมิภาค กลายเป็นตัวเด่นแทน
คำอธิบาย + ปัจจัยประกอบฉาก
การที่ปริมาณฝุ่นมีความสัมพันธ์กับช่วงเวลา สามารถอธิบายได้จากรอยต่อของชั้นบรรยากาศ ซึ่งจะเป็นขอบเขตที่ “ดัก” ฝุ่นเอาไว้ภายในชั้นบรรยากาศใกล้ระดับพื้นดิน พอถึงตอนเช้าที่ในเมืองเริ่มมีกิจกรรมต่าง ๆ เช่น การจราจร การก่อสร้าง ฯลฯ ฝุ่นจากภายในพื้นที่ ก็จะเริ่มถูกปล่อยออกมาผสมโรง ทำให้ปริมาณฝุ่นในบรรยากาศชั้นล่าง (ที่ถูกล็อกไว้) ไต่ระดับเพิ่มขึ้น
จนกระทั่งดวงอาทิตย์สาดส่องและอุณหภูมิที่ระดับพื้นดินค่อย ๆ สูงขึ้น อากาศร้อนที่ขยายตัวจะผลักดันให้รอยต่อของชั้นบรรยากาศขยับสูงขึ้นไป และขอบเขตที่ฝุ่นจากระดับพื้นดินจะแพร่ไปได้ก็สูงขึ้นไปด้วย บวกกับ ความเร็วลม ที่ระดับพื้นดินซึ่งจะเพิ่มขึ้นตามอุณหภูมิ สามารถพัดพาฝุ่นบางส่วนออกไปจากเขตเมือง จึงเป็นเหตุผลให้ความหนาแน่นของฝุ่นเริ่มลดลงในช่วงสาย ก่อนที่ทุกอย่างจะกลับคืนสภาพเดิมในช่วงหัวค่ำที่อุณหภูมิเริ่มลดลง
ประเด็นสำคัญ #4: ปัจจัยที่ส่งผลต่อปริมาณฝุ่น
ถึงตรงนี้เรามาสรุปกันดีกว่าว่าอะไรบ้างที่ส่งผลให้ปริมาณฝุ่น PM 2.5 ลดลง
- อุณหภูมิ – อุณหภูมิสูงทำให้รอยต่อของชั้นบรรยากาศสูงขึ้น
- ความเร็วลม – ลมแรงทำให้ระบายฝุ่นออกจากพื้นที่ได้มากขึ้น
- ทิศทางลม – ลมพัดเข้ามาจากพื้นที่ที่มีฝุ่นน้อย
- ปริมาณฝน – ปริมาณฝนที่มากทำให้ PM 2.5 ลดลง [ดูภาพประกอบ]
จากการเก็บข้อมูลที่เมืองเทียนจิน หลังจากฝนตกในวันที่ 22-24 กรกฎาคม ปรากฏว่าปริมาณฝุ่น PM 2.5 ในวันที่ 25 ลดลงอย่างฮวบฮาบ
งานวิจัยเกี่ยวกับฝนที่น่าสนใจอีกเรื่องหนึ่ง คือ ฝนสามารถลดปริมาณฝุ่น PM 2.5 ลดได้ราว 56 เปอร์เซ็นต์ สิ่งที่น่าแปลกใจอยู่ที่ว่าช่วง 1 ชั่วโมงแรกหลังฝนตก ปริมาณฝุ่นยังไม่เปลี่ยนแปลงเท่าใดนัก แต่หลังจากนั้นฝุ่นจะค่อย ๆ ลดลงใน 12 ชั่วโมงถัดมา คำถามที่ชวนให้คิด คือ ถ้าน้ำฝนสามารถชะล้างฝุ่นในอากาศได้โดยตรง ปริมาณฝุ่นควรจะลดลงโดยทันทีมิใช่หรือ? หรือหากไม่เป็นเช่นนั้น มีกลไกอะไรภายหลังฝนตกที่ทำให้ฝุ่นลดลง ...น่าเสียดายบทความทางวิชาการที่หยิบยกมาไม่ได้บอกตรงนี้ไว้
ประเด็นสำคัญ #5: ถ้าน้ำฝนไม่สามารถชะล้างฝุ่นในอากาศได้โดยตรง การบรรทุกน้ำมาฉีดพ่นไปในอากาศจะช่วยลดฝุ่นได้จริงหรือ
ถึงตรงนี้เราคงได้คำตอบแล้วว่า ฝุ่น PM 2.5 คืออะไร มาจากไหน ส่วนที่ว่าปีนี้ทำไมสถานการณ์จึงหนักกว่าที่ผ่านมา ก็น่าจะย้อนรอยจากปัจจัยเกื้อหนุนที่ได้กล่าวมาแล้ว ซึ่งได้แก่ อุณหภูมิ, กระแสลม, ปริมาณฝน รวมถึงปัจจัยตามฤดูกาลอื่น ๆ (เช่น ความกดอากาศ และความชื้น) ที่น่าจะเหมาะเจาะสำหรับการกักเก็บฝุ่น บวกกับความเป็นไปได้ที่กรุงเทพฯ และบริเวณโดยรอบเองก็มีการ “ผลิตฝุ่น” มากขึ้นด้วย เนื่องจากเราไม่ได้วางแผนระยะยาวที่ดีเพียงพอเอาไว้ตั้งแต่เมื่อหลายปีก่อน
โมเดลฝุ่น
เพื่อให้เห็นภาพอย่างเป็นรูปธรรม ผมอยากนำเสนอโมเดลอย่างง่ายที่อธิบายเรื่องฝุ่น PM 2.5 ตามภาพนี้
จะเห็นว่า input ของฝุ่น ได้แก่ ฝุ่นที่พัดหรือแพร่เข้ามาจากภูมิภาคข้างเคียง (A) และฝุ่นที่ก่อขึ้นมาจากในพื้นที่ (B) ส่วน output ของฝุ่น ได้แก่ ฝุ่นที่ถูกชะล้างหรือกำจัดไปในพื้นที่ (C) และฝุ่นที่พัดหรือแพร่ออกไปสู่ภูมิภาคข้างเคียง (D) ทั้งนี้ หากฝุ่นส่วนมากถูกดักเอาไว้ด้วยรอยต่อของชั้นบรรยากาศอย่างสมบูรณ์ เราจะสามารถเขียน ปริมาณฝุ่นที่เพิ่มขึ้นในพื้นที่ (T) ได้ว่า
T = A + B – C – D
เนื่องจาก A และ D เป็นส่วนที่ขึ้นอยู่กับกระแสลมและสภาพดินฟ้าอากาศตามฤดูกาล ซึ่งไม่สามารถควบคุมได้ เราจึงสามารถจัดรูปสมการข้างต้นใหม่ได้ว่า T = (A – D) + (B – C) โดยที่พจน์หลัง (B – C) เป็นฝุ่นส่วนที่สามารถบริหารจัดการได้ และเราจะมุ่งเน้นที่จุดนี้
ฝุ่นที่ก่อขึ้นจากในพื้นที่ (B) อาจมาจากยานพาหนะ ไม่ว่าจะเป็นการปล่อยไอเสีย การเสียดสีของยางรถ หรือฝุ่นที่เกิดขึ้นจากการเบรก, ฝุ่นคอนกรีตที่มาจากการก่อสร้าง, ฝุ่นที่ฟุ้งจากพื้นดิน, ฝุ่นจากโรงงานอุตสาหกรรม และฝุ่นที่มาจากการเผาในที่โล่งแจ้ง การตรวจวัดและจำแนกแหล่งที่มาของฝุ่นมีความสำคัญในแง่ที่ทำให้เราสามารถ “เลือกใช้” มาตรการที่หนักเบาตามระดับการก่อฝุ่นได้อย่างเหมาะสม
ตัวอย่างเช่น สมมติว่าฝุ่นจากการก่อสร้างมีสัดส่วน 40 เปอร์เซ็นต์ ภาครัฐอาจเพิ่มความเข้มงวดและสั่งให้หยุดการก่อสร้าง หากพบว่าเขตก่อสร้างใดปล่อยฝุ่นออกมาเกินมาตรฐาน ขณะเดียวกันก็ไม่จำเป็นต้องไปสั่งหยุดโรงงาน หากฝุ่นจากแหล่งดังกล่าวมีสัดส่วนน้อยจนได้ไม่คุ้มเสีย อย่างนี้เป็นต้น
สำหรับฝุ่นที่ถูกชะล้างหรือกำจัดไปในพื้นที่ (C) อาจเกิดขึ้นเองตามธรรมชาติ เช่น ฝนตก หรือเกิดจากการกระทำของมนุษย์ เช่น การกำจัดฝุ่นด้วยเครื่องมือ การล้างทำความสะอาด และการพ่นละอองน้ำหรือสารเคมีเพื่อดักจับฝุ่นในอากาศ
เมื่อใดก็ตามที่อัตราเร็วในการชะล้าง/กำจัดฝุ่น สูงกว่าอัตราเร็วในการสร้างฝุ่นใหม่ (C > B) เช่น กรณีที่ฝนตกแรง ๆ ปริมาณฝุ่นที่เพิ่มขึ้นในพื้นที่ หรือ T ก็จะติดลบ (สมมติในเบื้องต้นว่าผลรวมของฝุ่นที่เข้าและออกจากภูมิภาคข้างเคียงเป็นศูนย์ คือ A = D) นั่นหมายความว่า ปริมาณฝุ่นในพื้นที่จะลดลง ในทางคณิตศาสตร์ เหตุการณ์เช่นนี้อาจเกิดขึ้นได้ถ้าตัว C มีค่ามาก หรือไม่ก็ตัว B มีค่าน้อย หรือทั้งสองอย่าง
มีข้อสังเกตสองประการที่น่าสนใจ (แต่อาจไม่เป็นจริงก็ได้) ประการหนึ่ง คือ เป็นไปได้หรือไม่ว่าฝนที่ตกลงมาอาจไม่ได้ชะล้างฝุ่นละอองในอากาศโดยตรง สอดคล้องกับข้อเท็จจริงที่ว่าปริมาณฝุ่นไม่ได้ลดลงโดยทันทีหลังฝนหยุด แต่ฝนอาจไปชะล้างฝุ่นบนถนนและพื้นดินจนไม่สามารถฟุ้งกลับขึ้นมาใหม่ ซึ่งเป็นการลดตัว B มากกว่าที่จะไปเพิ่มตัว C
ประการที่สอง เป็นข้อสังเกตของ โธมัส ทาลเฮล์ม อาจารย์จากวิทยาลัยธุรกิจของมหาวิทยาลัยชิคาโก ซึ่งสังเกตว่าฝนที่ตกหนักในกรุงปักกิ่งบางครั้งก็ไม่ได้ช่วยให้ฝุ่น PM 2.5 ลดลง พร้อมกับอ้างอิงผลการศึกษาจากประเทศจีนที่พบว่าฝนช่วยชะล้างฝุ่นอนุภาคใหญ่ได้ แต่ไม่ค่อยมีผลต่อฝุ่นอนุภาคเล็ก ทาลเฮล์มตั้งข้อสังเกตว่าบางที “ลม” ที่มาพร้อมกับฝนมากกว่าที่เป็นตัวพัดพาฝุ่นออกไป ซึ่งแบบนี้ก็หมายความว่า D > A และส่งผลให้ T ติดลบได้เหมือนกัน
ประเด็นสำคัญ #5 (new): น้ำฝนและการฉีดพ่นน้ำไม่น่าจะสามารถชะล้างฝุ่น PM 2.5 ในอากาศได้โดยตรง
นอกบ้าน vs ในบ้าน
การกำจัดฝุ่น PM 2.5 นอกบ้านภายในระยะเวลาอันสั้น ดูเหมือนจะเป็นสิ่งที่ทำได้ยากมากหรือแทบจะเป็นไปไม่ได้ ทางเลือกของประชาชนทั่วไปจึงอยู่ที่
- การปรับพฤติกรรมให้สอดคล้องกับคุณภาพอากาศนอกบ้าน เช่น หลีกเลี่ยงการออกจากบ้านในช่วงเช้า (ถ้าทำได้), ใส่หน้ากากป้องกันมลพิษ และลดระยะเวลาที่ต้องอยู่นอกบ้าน
- ปรับปรุงคุณภาพของอากาศภายในบ้านหรืออาคาร
มีผลการศึกษาระบุว่าผู้คน 60 เปอร์เซ็นต์จะใช้วิธี “ปิดหน้าต่าง” เมื่อคุณภาพอากาศแย่ แต่แม้จะทำเช่นนั้น 54-63% ของฝุ่น PM 2.5 ภายในอาคาร ก็เป็นฝุ่นที่มาจากนอกอาคารอยู่ดี และยิ่งถ้าเปิดหน้าต่าง ตัวเลขก็จะขยับขึ้นเป็น 92% โน่นเลย สรุปง่าย ๆ ก็คือ อากาศภายในอาคารจะดีหรือแย่ไปตามอากาศนอกอาคาร เพียงแต่จะดีเลย์หรือช้ากว่ากันประมาณ 1-2 ชั่วโมง
หากจะกล่าวโดยทั่วไป ฝุ่น PM 2.5 สามารถเกิดขึ้นภายในอาคารเอง เช่น จากการหุงต้มอาหาร การล้างทำความสะอาด และจากกิจกรรมต่าง ๆ อย่างการจุดยากันยุงแบบขด หลายท่านไม่ทราบว่ายาจุดกันยุงแบบนี้สร้างฝุ่น PM 2.5 ได้ถึง 626 ไมโครกรัม/ลูกบาศก์เมตร หรือสูงเกินมาตรฐานความปลอดภัยของประเทศไทยกว่า 11 เท่าตัว นี่เป็นสิ่งที่ไม่ควรมองข้าม
ประเด็นสำคัญ #6: ถ้าไม่รู้จะทำอย่างไร อย่างน้อยปิดหน้าต่างก็ช่วยได้มาก ขณะเดียวกันก็ระวังไม่ทำกิจกรรมที่จะสร้างฝุ่น PM 2.5 ภายในอาคารเสียเอง
สำหรับฝุ่น PM 2.5 จากนอกอาคาร นอกจากจะผ่านเข้ามาทางหน้าต่างหรือช่องเปิดต่าง ๆ แล้ว ยังสามารถแทรกซึมผ่านช่องหรือรอยแตกของอาคารเข้ามาได้ด้วย บางท่านอาจเข้าใจว่ารอยแตกหรือช่องตามขอบประตู/หน้าต่างเหล่านั้นเล็กนิดเดียว ไม่น่าจะมีผลอะไร แต่ในความเป็นจริงอากาศ (และฝุ่น) สามารถผ่านเข้ามาในอาคารได้อย่างต่อเนื่องไม่หยุดหย่อน โดยรวมแล้วจึงส่งผลต่อคุณภาพอากาศภายในอาคารได้มากทีเดียว
ปัจจัยที่ทำให้ฝุ่นสามารถซึมผ่านช่องหรือรอยแตกได้มากหรือน้อย ประกอบด้วย
- ขนาดอนุภาค – ฝุ่นอนุภาคเล็กสามารถแทรกตัวเข้ามาได้โดยสะดวกมากกว่าฝุ่นที่มีอนุภาคใหญ่
- ความดันอากาศ – หากความดันอากาศภายนอกสูงกว่าภายใน (เช่น เมื่อภายนอกมีอากาศนิ่ง แต่ภายในอาคารเป็นอากาศไหล) การแทรกซึมเข้าสู่ภายในอาคารจะมีมากขึ้น
- รูปทรงของช่องหรือรอยแตก – หากเป็นช่องตรง ๆ ฝุ่นจะสามารถผ่านได้สะดวกกว่าช่องซิกแซกหรือมีเหลี่ยมมุม
- ผิวสัมผัสของรอยแตก – หากรอยแตกมีผิวค่อนข้างเรียบ การแทรกซึมจะเป็นไปได้ง่ายกว่า
ประเด็นสำคัญ #7: การซ่อมแซมรอยแตกและปิดช่องต่าง ๆ เตรียมเอาไว้ก่อนอาจเป็นความคิดที่ดี
ทั้งหมดที่ว่ามานี้เป็นมาตรการสำหรับ “บรรเทา” ฝุ่น PM 2.5 ภายในอาคาร ซึ่งอาจช่วยยืดระยะเวลาที่ฝุ่นจะบุกเข้ามาในบ้านได้ แต่ถ้าจะให้ดีจริง ๆ ควรมีการติดตั้งเครื่องกรองอากาศที่สามารถกรองฝุ่นอนุภาคเล็ก เหมาะสมกับพื้นที่ใช้งาน และเหมาะสมกับเงินในกระเป๋าด้วย
หวังว่าเนื้อหานี้จะเป็นประโยชน์สำหรับทุกท่านที่ต้องเผชิญกับฝุ่นจิ๋วในปีนี้และปีต่อ ๆ ไปครับ
------------------------------------------
เอกสารอ้างอิง ตัวเลขและภาพประกอบ (ยกเว้นภาพโมเดล) มาจากเอกสารต่อไปนี้
[หมายเหตุ: ภาพประกอบบางภาพมีการปรับปรุงเพื่อให้อ่านง่ายขึ้น]
Yaolin Lin et al., A Review of Recent Advances in Research on PM2.5 in China, International Journal of Environmental Research and Public Health
Han et al., Evaluation of Regional Background Particulate Matter Concentration based on Vertical Distribution Characteristics, Atmospheric Chemistry and Physics
Feng and Wang, Influence of different weather events on concentrations of particulate matter with different sizes in Lanzhou, China, Journal of Environmental Sciences
วันศุกร์ที่ 1 กุมภาพันธ์ พ.ศ. 2562
ตัวเลขน่ารู้ - ฝุ่น PM 2.5
ในสถานการณ์ที่กรุงเทพฯ ปกคลุมไปด้วยฝุ่นละออง โดยเฉพาะฝุ่น “ขนาดจิ๋ว” ที่มีขนาดอนุภาคเล็กกว่า 2.5 ไมโครเมตร หรือที่เรียกกันว่า PM 2.5 เราจึงควรถือโอกาสนี้ศึกษาและหาทางรับมือกับฝุ่นพิษดังกล่าวอย่างเป็นรูปธรรม สำหรับบทความนี้จะเป็นเรื่องราวของตัวเลขที่เกี่ยวข้อง ส่วนประเด็นอื่น ๆ เช่น พิษภัยของฝุ่น, หน้ากากกรองอนุภาค ฯลฯ คิดว่าท่านทั้งหลายคงหาอ่านได้ไม่ยาก
[ข้อมูลต่อไปนี้เป็นสิ่งที่ผู้เขียนเรียบเรียงและอธิบายด้วยภาษาง่าย ๆ เพื่อเป็นประโยชน์ต่อสาธารณชน ผู้อ่านควรตรวจสอบกับแหล่งความรู้ทางวิชาการก่อนนำไปใช้อ้างอิง]
แค่ไหนถึงอันตราย
ความจริงแล้วมลพิษในอากาศมีอยู่มากมาย แต่ที่กำลังคุกคามและสร้างปัญหาใหญ่อยู่ก็คือ ฝุ่นละอองขนาดเล็ก (Particulate Matter หรือ PM) โดยเฉพาะ PM 2.5 หรือฝุ่นที่มีอนุภาคเล็กกว่า 2.5 ไมโครเมตร ด้วยขนาดที่เล็กมาก ๆ เพียงประมาณเศษ 1 ส่วน 30 ของขนาดเส้นผมคนเรา ฝุ่นละอองนี้จึงสามารถหลุดรอดผ่านการดักจับของระบบทางเดินหายใจเข้าสู่เส้นเลือด และไปทำอันตรายต่อร่างกายได้มาก โดยองค์การอนามัยโลกได้จัดให้ฝุ่น PM 2.5 เป็นสารก่อมะเร็งอย่างหนึ่งด้วย
ปริมาณฝุ่นสามารถวัดในหน่วย ไมโครกรัม/ลูกบาศก์เมตร โดยวัดเป็นค่าเฉลี่ย 24 ชั่วโมง หรือค่าเฉลี่ย 1 ปี ส่วนการกำหนดมาตรฐานความปลอดภัยว่าระดับใดจะเริ่มเป็นอันตรายนั้นขึ้นอยู่กับแต่ละประเทศ ดังตารางด้านล่างนี้
ดัชนีชี้อันตราย
ในอีกทางหนึ่ง นอกจากการวัดปริมาณฝุ่นเป็น ไมโครกรัม/ลูกบาศก์เมตร แล้ว ยังมีการวัดค่าในรูปแบบของดัชนีด้วย อย่างเช่น AQI หรือ Air Quality Index ซึ่งเป็นดัชนีหรือ “ตัวเลข” ที่คำนวณขึ้นมาและสามารถเทียบเคียงกับปริมาณฝุ่น PM 2.5 ตามหน่วยวัดไมโครกรัม/ลูกบาศก์เมตรได้ (ต่อไปนี้จะขอเรียกย่อ ๆ ว่า ไมโครกรัมฯ เพื่อไม่ให้ยืดยาวเกินไป)
ข้อควรสังเกต สำหรับชาวบ้านทั่วไป เมื่อได้ยินค่าตัวเลขจากสื่อต่าง ๆ เช่น 50, 70 หรือ 110
- ให้พิจารณาว่าตัวเลขดังกล่าวเป็น ค่าดัชนี (AQI) หรือ ปริมาณฝุ่น (ไมโครกรัมฯ) กันแน่ เพราะนี่เป็นการพูดถึงสิ่งเดียวกันในสองรูปแบบ และแน่นอนความหมายนั้นแตกต่างกัน
- หากเป็นค่า AQI ท่านต้องตระหนักว่าเป็น AQI ของใคร? อย่างตารางทั้งสองด้านล่างนี้ ฝั่งซ้ายเป็นตาราง AQI ของไทยจากกรมควบคุมมลพิษ ส่วนฝั่งขวาเป็นตาราง AQI ของสหรัฐอเมริกาจากเว็บไซต์ Wikipedia
- ค่า AQI อาจไม่บ่งบอกถึงปริมาณฝุ่น PM 2.5 เสมอไป เพราะดัชนีดังกล่าวคำนวณมาจากสารพิษในอากาศหลายตัว ไม่ว่าจะเป็น SO2, NO2, ก๊าซโอโซน ฯลฯ แล้วอิงตามตัวที่มีปริมาณเป็นพิษมากที่สุด ดังนั้น ค่า AQI ที่สูง ณ เวลาหนึ่ง ๆ อาจเป็นผลมาจากสารพิษตัวอื่นที่ไม่ใช่ฝุ่น PM 2.5 ก็ได้
- ปริมาณฝุ่นที่วัดเป็นค่าเฉลี่ย 24 ชั่วโมง หมายถึง หน่วยงานที่เกี่ยวข้องทำการวัดปริมาณฝุ่นย้อนหลังไปเป็นเวลา 24 ชั่วโมง (นับจากเวลาที่มีรายงานออกมา) จึงอาจไม่สะท้อนสถานการณ์ที่เป็นปัจจุบัน แต่ก็มีข้อดีที่ความแม่นยำ ตัวอย่างเช่น การวัดค่าอากาศเฉลี่ยย้อนหลัง 24 ชั่วโมงอาจมีความคลาดเคลื่อนในระดับ 0.5 ไมโครกรัม/ลูกบาศก์เมตร แต่การวัดค่าเฉลี่ยย้อนหลังเพียง 1 ชั่วโมงอาจมีความคลาดเคลื่อน 1.5 ไมโครกรัม/ลูกบาศก์เมตร ส่วนการวัดเพียงครั้งเดียว (ไม่มีการเฉลี่ย) ก็จะยิ่งคลาดเคลื่อนมากไปกว่านั้น

สังเกตว่า AQI = 50 ของไทยจะเทียบเท่าฝุ่น PM 2.5 จำนวน 37 ไมโครกรัม/ลูกบาศก์เมตร ส่วน AQI = 50 ของอเมริกาจะเทียบเท่า 12 ไมโครกรัม/ลูกบาศก์เมตรเท่านั้น ถ้าอยากคุยให้รู้เรื่องตรงกันแน่ ๆ ก็เรียกเป็นไมโครกรัมฯ ไปเลย จะได้ลดความสับสน
สรุปง่าย ๆ ก็คือ ควรเจาะจงวัดปริมาณฝุ่น PM 2.5 เป็นไมโครกรัมฯ ไปเลย และถ้านับตามมาตรฐานไทย ทุกคนจะปลอดภัย เมื่อปริมาณฝุ่นไม่เกิน 37 ไมโครกรัม/ลูกบาศก์เมตร
วันศุกร์ที่ 11 มกราคม พ.ศ. 2562
ต้องเฉลี่ย หรือ ไม่ต้องเฉลี่ย
อัตราส่วนทางการเงิน เป็นเครื่องมือสำคัญสำหรับการลงทุน และส่วนใหญ่ก็ได้จากการจับตัวเลขบางตัวมาหารกันนั่นเอง นักลงทุนที่อ่านหนังสือมามากจะทราบดีว่า สูตรของอัตราส่วนตัวเดียวกันอาจมีทั้งแบบเรียบง่ายและซับซ้อน ขึ้นอยู่กับ “ความเยอะ” ของผู้นิยาม รวมถึงวัตถุประสงค์การนำไปใช้
ตัวอย่างของเรื่องนี้ เช่น อัตราส่วนผลตอบแทนต่อสินทรัพย์ (Return on Assets หรือ ROA) มีสูตรคำนวณง่าย ๆ ที่เปิดหาจากเว็บไซต์ Investopedia ได้ว่า
สินทรัพย์... ตอนไหน?
ปัญหาคลาสสิกของอัตราส่วนลักษณะนี้มักอยู่ที่ ตัวส่วน มากกว่าตัวเศษ เพราะตัวเศษ (กำไรสุทธิ) นั้นโกยมาทั้งปีก็มีค่าเดียว แต่ตัวส่วนอาจเป็นได้ทั้งสินทรัพย์ตอนต้นปีหรือปลายปี หรือบางแนวคิดก็ให้จับตัวเลขต้นปีกับปลายปีมาเฉลี่ยกันก็มี อย่างเช่น สูตรจากเว็บไซต์ Wikipedia
แนวคิดที่แพร่หลายสำหรับประเด็นนี้ ได้แก่
- ใช้สินทรัพย์ต้นปี – โดยให้เหตุผลว่าเป็นสินทรัพย์ที่มีอยู่ ณ จุดตั้งต้นของการดำเนินงานทั้งหมดในปีนั้น
- ใช้สินทรัพย์ปลายปี – โดยอาศัยความที่เป็นตัวเลขหาง่าย เพราะข้อมูลสรุปทางการเงินของบริษัทต่าง ๆ มักรายงานกำไรประจำปีและสินทรัพย์ปลายงวดมาพร้อมกันในคอลัมน์เดียวกันอยู่แล้ว
- ใช้สินทรัพย์เฉลี่ย – โดยให้เหตุผลว่าสินทรัพย์ของบริษัทมักมีการเปลี่ยนแปลงในระหว่างปี และการใช้ค่าเฉลี่ยก็จะสะท้อนสินทรัพย์ที่บริษัทใช้จริงได้มากที่สุด
นักลงทุนโดยทั่วไปมักเข้าใจว่าข้อ 3 เป็นแนวทางที่ถูกต้องที่สุด ส่วนข้อ 1 ก็ถือว่ามีเหตุผล แต่ไม่ค่อยละเอียดลออ และที่ไม่เข้าท่าที่สุดก็ดูเหมือนจะเป็นข้อ 2
อย่างไรก็ตาม หากเราทำความเข้าใจ “วัตถุประสงค์” ของการใช้อัตราส่วนทางการเงินในแต่ละรูปแบบ แต่ละข้อต่างล้วนมีข้อดีอยู่ในตัว แม้กระทั่งผมเองก็คำนวณ ROA แบบเร็ว ๆ ตามข้อ 2 อยู่บ่อยครั้ง หากต้องการมองภาพธุรกิจอย่างคร่าว ๆ รวมถึงเปรียบเทียบพัฒนาการของบริษัทในแต่ละปี ซึ่งกิจกรรมแบบนี้ไม่จำเป็นต้องใช้ตัวเลขที่แม่นยำมากมายอะไรนัก
ว่าด้วยความถูกต้อง
ถัดจากความง่าย ถ้าเราหันมาคำนึงถึงความถูกต้องกันบ้าง คำถามที่ผุดขึ้นต่อมาก็คือ การหาค่าเฉลี่ยจะให้ผลลัพธ์ที่ถูกต้องกว่าจริง ๆ น่ะหรือ
หากจินตนาการถึงบริษัทแห่งหนึ่งที่มีสินทรัพย์ 100 ล้านบาทตอนต้นปี และเพิ่มขึ้นเป็น 106 ล้านบาทตอนสิ้นปี โดยในปีนั้นบริษัทมีกำไรสุทธิ 12 ล้านบาท
ถ้าเราคำนวณ ROA จากสินทรัพย์ต้นปี จะได้เท่ากับ 12 / 100 = 12 เปอร์เซ็นต์ แต่ถ้าเราคำนวณจากสินทรัพย์เฉลี่ย (100 + 106) / 2 = 103 ล้านบาท ROA จะกลายเป็น 12 / 103 = 11.65 เปอร์เซ็นต์
เมื่อได้ตัวเลขดังนี้ นักลงทุนทั่วไปมักไม่ใส่ใจและสรุปทันทีว่าตัวเลขหลังถูกต้องกว่า แต่ถ้าเราเจาะเข้าไปในรายละเอียด และสมมติว่าสินทรัพย์ 6 ล้านบาทที่เพิ่มขึ้นในระหว่างปีเป็นการเพิ่มขึ้นโดยเท่า ๆ กันเฉลี่ยเดือนละ 0.5 ล้านบาท เราจะได้มุมมองต่อสินทรัพย์ดังแผนภาพ
เราจะสามารถบอกได้ว่า กำไรที่บริษัททำได้ในเดือนมกราคมเกิดจากสินทรัพย์ 100 ล้านบาทที่มีอยู่ในเดือนนั้น ส่วนกำไรของเดือนกุมภาพันธ์ก็เกิดจากสินทรัพย์ 100.5 ล้านบาท และกำไรของเดือนมีนาคมก็เกิดจากสินทรัพย์ 101.0 ล้านบาท อย่างนี้เป็นต้น (การใช้สีที่แตกต่างกัน เพื่อให้ผู้อ่านสามารถมองเป็นไตรมาสและแยกเดือนต่าง ๆ ได้ง่ายขึ้น)
เพิ่มความซับซ้อน สะท้อนชีวิตจริง
ตัวอย่างนี้จะซับซ้อนมากขึ้น หากเราพิจารณาประเด็นเรื่องการจ่ายเงินปันผลในช่วงกลางปี สมมติว่าบริษัทจ่ายเงินปันผล 6 ล้านบาท นักลงทุนจะเห็นว่าจริง ๆ แล้วสินทรัพย์ของบริษัทควรมีการเติบโตไปกับกำไรที่บริษัททำได้ เช่น เฉลี่ยเดือนละ 1 ล้านบาท (แทนที่จะเป็น 0.5 ล้านบาท อย่างที่สมมติกันไปในตอนแรก) และพอสิ้นเดือนมิถุนายน บริษัทก็จ่ายปันผลออกมาเป็นเงินสด ทำให้สินทรัพย์ของบริษัทลดฮวบก่อนจะฟื้นตัวขึ้นมาใหม่อีกรอบหนึ่งจนเป็น 106 ล้านบาท ณ สิ้นเดือนธันวาคม ดังแผนภาพ
สังเกตว่าการจ่ายเงินปันผล ณ สิ้นเดือนมิถุนายน ทำให้สินทรัพย์ ณ ต้นเดือนกรกฎาคม (แท่งที่ 7) ที่น่าจะเป็น 106.0 ล้านบาท ลดฮวบลงไปเหลือเพียง 100.0 ล้านบาท ก่อนจะเดินหน้าสะสมสินทรัพย์ขึ้นมาใหม่หลังจากนั้น
นอกจากการจ่ายเงินปันผลแล้ว อีกประเด็นหนึ่งที่นักลงทุนควรคำนึงถึงด้วย คือ กำไรที่บริษัทสร้างได้ในแต่ละเดือนอาจไม่ใช่ผลจากสินทรัพย์ของเดือนนั้น ๆ ทว่าอาจเริ่มต้นมาจากการสั่งซื้อวัตถุดิบเมื่อสองหรือสามเดือนก่อนหน้า (ระยะเวลาจะยาวหรือสั้นจำเป็นต้องศึกษาจาก วงจรเงินสด และ วงจรการดำเนินงาน ของบริษัท) เพื่อให้เข้าใจประเด็นนี้โดยไม่ต้องลงลึกมากจนเกินไป สมมติว่ากำไรของบริษัทในแต่ละเดือนเกิดจากการเริ่มต้นใช้สินทรัพย์ตั้งแต่สองเดือนก่อนหน้า สินทรัพย์ที่บริษัทใช้สร้างกำไรสำหรับปีจะเป็นไปตามแผนภาพ
กล่าวคือ กำไรของเดือนมกราคมเกิดจากการใช้สินทรัพย์ตั้งแต่เดือนพฤศจิกายนปีก่อน ส่วนกำไรของเดือนกุมภาพันธ์ก็เกิดจากการใช้สินทรัพย์ตั้งแต่เดือนธันวาคมปีก่อน... อย่างนี้เรื่อยไปจนถึงกำไรของเดือนธันวาคมปีปัจจุบันเกิดจากการใช้สินทรัพย์ในเดือนตุลาคม
หากจะดูสินทรัพย์ที่ใช้จริง เราก็ต้องเฉลี่ยตัวเลขทั้งหมด 12 ตัว คือ
(98 + 99 + 100 + 101 + 102 + 103 + 104 + 105 + 100 + 101 + 102 + 103) / 12
จะได้สินทรัพย์ที่ใช้จริงเฉลี่ยเท่ากับ 101.5 ล้านบาท และถ้านำตัวเลขนี้ย้อนกลับไปคำนวณ ROA ใหม่ก็จะได้เท่ากับ 12 / 101.5 = 11.82 เปอร์เซ็นต์ เทียบกับตัวเลขเดิมที่เคยคำนวณไว้ตั้งแต่แรก (ลืมกันไปแล้วหรือยัง?) 12 เปอร์เซ็นต์ กับ 11.65 เปอร์เซ็นต์
สรุป
การคำนวณอัตราส่วนทั้งสองแบบ คือ แบบที่ใช้ตัวเลขต้นปี และแบบที่ใช้ค่าเฉลี่ยต้นปีกับปลายปี ล้วนมีความคลาดเคลื่อนเกิดขึ้นด้วยกันทั้งสิ้น นักลงทุนอาจทดลองปรับเปลี่ยนสมมติฐานแล้วดูว่ากรณีของบริษัทที่เราสนใจนั้นเป็นอย่างไร เพื่อจะได้รู้ผลลัพธ์ที่เฉพาะเจาะจงและตัดสินใจได้ดีขึ้น
อย่างไรก็ตาม สำหรับตัวอย่างนี้ ในเมื่อตัวเลขจากทั้งสองวิธีมีความผิดพลาดเล็กน้อยใกล้เคียงกัน ความเห็นโดยส่วนตัวของผม ก็คือ ไม่ต้องไปเสียเวลาหาค่าเฉลี่ยให้ยุ่งยากและสุ่มเสี่ยงที่จะคำนวณผิดพลาดมากขึ้นหรอก คำนวณด้วยตัวเลขต้นปีไปนั่นแหละ ส่วนท่านอื่นจะเลือกแบบไหนก็ตามอัธยาศัย เพราะจุดประสงค์ของบทความนี้ก็เพียงเพื่อจะบอกทุกท่านว่า การทำอะไร “เยอะ ๆ” นั้นอาจจะไม่ได้ผลลัพธ์ที่ดีกว่าอย่างมีนัยสำคัญจนคุ้มค่ากับความวุ่นวายที่เพิ่มขึ้นเสมอไป
วันเสาร์ที่ 5 มกราคม พ.ศ. 2562
ไฟไหม้มัดข้าว
ย้อนไป 164 ปีที่แล้วในช่วงเย็นวันหนึ่งก่อนสิ้นปี ขณะที่ชาวบ้านฮิโระมุระกำลังง่วนอยู่กับการจัดเตรียมงานเฉลิมฉลองเทศกาลเก็บเกี่ยว จนแทบไม่มีใครรู้สึกถึง "แผ่นดินไหว" ที่เพิ่งเกิดขึ้นสด ๆ ร้อน ๆ
โกเรียว ฮามะกุจิ ผู้นำหมู่บ้านสังเกตว่าแผ่นดินไหวครั้งนั้นแม้ไม่รุนแรง แต่การสั่นไหวก็เกิดขึ้นช้าและยาวนานผิดประหลาด เมื่อออกจากบ้านและมองมาที่ทะเล เขาพบว่าระดับน้ำได้ลดลงจนเนินหินบริเวณชายฝั่งปรากฏขึ้น โกเรียวรู้ทันทีว่าสึนามิกำลังมาแล้ว
เพื่อช่วยชีวิตผู้คนในหมู่บ้าน เขาตัดสินใจจุดไฟเผากองฟ่อนข้าวที่เก็บเกี่ยวมาโดยทันที เมื่อไฟกองใหญ่ลุกลามขึ้นประกอบกับท้องฟ้าที่ค่อย ๆ มืดลงขณะที่ตะวันตกดิน ชาวบ้านที่หอสังเกตการณ์ก็ส่งสัญญาณเรียกทุกคนให้รีบมาช่วยกันดับไฟที่บ้านของโกเรียว พวกคนหนุ่มที่วิ่งมาถึงก่อนพยายามจะเข้าไปดับไฟ แต่โกเรียวก็ตะโกนห้ามไว้ท่ามกลางความประหลาดใจของทุกคน
เมื่อชาวบ้านทยอยกันมาถึงบ้านโกเรียวที่เนินเขาจนครบแล้ว โกเรียวบอกให้ทุกคนมองไปที่ทะเล สิ่งที่ปรากฏต่อสายตา คือ แนวคลื่นยักษ์ที่ก่อตัวเป็นกำแพงทะมึนอยู่ตรงขอบฟ้า ไม่นานคลื่นสึนามิก็ถาโถมเข้าสู่หมู่บ้านและกวาดทุกอย่างจนราบเป็นหน้ากลอง อย่างไรก็ตาม โกเรียวสามารถรักษา 400 ชีวิตในหมู่บ้านเอาไว้ได้
-------------------------------------------
นี่เป็นเรื่องราวโดยย่อของเหตุการณ์ "ไฟไหม้มัดข้าว" (the fire of rice sheaves) ตามที่ปรากฏในหนังสือแบบเรียนชั้นประถมศึกษาของประเทศญี่ปุ่น โดยจุดเริ่มต้นในการค้นหาข้อมูลมาจากบทความในวารสารอินทาเนียที่ผมอ่านเมื่อไม่นานมานี้
ท่านทั้งหลายคิดอย่างไรบ้าง? ข้าวกองใหญ่แลกกับชีวิตชาวบ้านหลายร้อยคน
ผมเชื่อว่าคนจำนวนมากจะบอกว่า "สุดแสนจะคุ้ม" เพราะหากใช้วิธีวิ่งไปบอกทุกคนตามบ้าน มันก็คงช้ามาก บางทีอาจมีคนมัวเก็บข้าวเก็บของไม่ยอมหนีภัยในทันที หรืออาจมีคนที่ออกไปธุระนอกบ้านจนตามหากันไม่เจอ ฯลฯ
แต่ในทางตรงข้ามคนอีกกลุ่มหนึ่งก็อาจจะอ้างว่า คนเรามีสิทธิ์เลือกรักษาทรัพย์สินของตนเองโดยชอบธรรม ส่วนการช่วยเหลือผู้คนก็เป็นความสำคัญลำดับรอง ๆ ลงมา
ข้อคิดที่ได้จากเรื่องนี้ คือ โลกของเรามีทั้งคนที่ถือประโยชน์ส่วนรวมเป็นสำคัญ (แบบโกเรียว) และคนที่ถือประโยชน์ส่วนตัวเป็นใหญ่ การที่ใครจะเลือกเป็นแบบไหนนั้นขึ้นอยู่กับว่าเขา "ให้คุณค่า" กับสิ่งใด
คนที่ให้คุณค่ากับความร่ำรวยจะใช้เงินเป็นไม้บรรทัด ถ้าท่านจนกว่าเขา เขาก็จะบอกว่าท่านด้อยกว่า หรือถ้าเอาวุฒิการศึกษาเป็นไม้บรรทัด หากท่านเรียนมาน้อยกว่าเขา เขาก็จะบอกว่าท่านด้อยกว่า
จุดสำคัญก็คือ ขอให้เราดีพอในโลกของเรา ตามไม้บรรทัดของเรา ส่วนจะยาวหรือสั้นในโลกของใครก็ไม่เป็นไร และในทางกลับกันเราก็ต้องระมัดระวังไม่ "ยัดเยียด" ไม้บรรทัดของเราให้กับคนอื่นด้วย
สุดท้ายที่ผมอยากให้ข้อสังเกตไว้ คือ การช่วยเหลือคนอื่น น่าจะเป็นไม้บรรทัดของหมู่บ้านฮิโระมุระนี้ - โกเรียวยอมสละข้าว ซึ่งอาจจะเป็นข้าวทั้งหมดของตัวเอง เพื่อช่วยเหลือคนอื่น ส่วนคนอื่นที่จริงก็เร่งรีบมาเพื่อจะช่วยโกเรียวดับไฟ
และในที่สุดแล้วความคิดที่จะช่วยเหลือคนอื่นนี่เองที่ทำให้ทุกคนรอดตาย
สมัครสมาชิก:
ความคิดเห็น (Atom)