เป็นที่เชื่อกันโดยทั่วไปว่าเราจำเป็นต้องมีเงินก้อนใหญ่ เพื่อเอาไว้แทะกินหลังเกษียณ บางกระแสระบุว่าจำนวนเงินขั้นต่ำ คือ 4 ล้านบาท แต่ถ้าอยากให้ชีวิตมีคุณภาพ ก็อาจต้องมีถึง 10 ล้านบาท โดย “ดีไซน์” ของการเกษียณในรูปแบบนี้อยู่ตรงที่การทยอยใช้เงินก้อนดังกล่าว และหวังว่าจะไม่หมดเงินก่อนหมดลม
เคยได้ยินไหมครับ ที่เขาบอกว่า “สุดเสียดาย ตายไปยังใช้เงินไม่หมด” กับ “สุดสลด ใช้เงินจนหมดแล้วยังไม่ตาย”
คำถามที่เกิดขึ้นในใจของผม คือ ชีวิตของเราควรจะลุ้นขนาดนั้นเชียวหรือ? และหากมีถึง 10 ล้านบาทจริง เรายังจำเป็นต้องนั่งแทะเงินด้วยใจตุ๊ม ๆ ต่อม ๆ อีกไหม หรือที่จริงเราสามารถเอาเงินก้อนที่ว่ามาสร้างกระแสเงินสดไว้เลี้ยงตัวได้ตลอดชีพสบาย ๆ... และจุดแบ่ง (ว่าจะแทะหรือไม่แทะ) มันอยู่ตรงไหน?
โมเดลการเลี้ยงชีพ
เพื่อตอบคำถามข้างต้น ผมได้สร้างโมเดลที่จะค้นหาความจริง โดยกำหนดให้ชาวเกษียณมีรายได้สองทาง ได้แก่
- กระแสเงินสดที่ไม่ต้องออกแรงทำงาน (Passive Cash Flow หรือ P) และ
- เงินที่ทยอยไถ่ถอนมาจากเงินก้อน (Cash Redemption หรือ R)
เมื่อนำรายได้ข้างต้นหัก ค่าใช้จ่าย (Expense หรือ X) เรียบร้อยแล้ว หากมีเงินสดเหลือ เราจะเรียกว่า Cash Leftover หรือ L ซึ่งทั้งหมดจะสามารถเขียนเป็นสมการการใช้เงินของชาวเกษียณในปีที่ 1 ได้ดังนี้
สังเกตว่าในสมการ เราคำนึงถึงเงินสดที่เหลือมาจากปีก่อนหน้า (ปีที่ศูนย์) หรือ L0 ด้วย
จากแนวคิดนี้ เราสามารถเขียนสมการให้อยู่ใน รูปทั่วไป ก็ได้ โดยตัวเลข 1 ที่ห้อยไว้เพื่อแสดงว่าเป็นปีที่ 1 ก็จะเปลี่ยนเป็น i และท่านก็จะสามารถแทนค่า i ให้เป็นตัวเลขปีใด ๆ ที่ท่านต้องการ
เมื่อย้ายข้างจัดรูปเสียหน่อยก็จะได้
หากสังเกตให้ดี ฝั่งขวาของสมการเป็นกระแสเงินสดที่ไหลเข้าและไหลออกในปีนั้น ๆ ส่วนฝั่งซ้ายก็เป็นการสรุปว่าเงินสดที่คงค้างอยู่ในระบบมีการเปลี่ยนแปลงไปเท่าไร
ภาพรวมหลังเกษียณ
แน่นอนว่าความสนใจของเรา ไม่ใช่ ชีวิตหลังเกษียณปีใดปีหนึ่ง แต่เป็นภาพรวมของทุก ๆ ปีภายหลังเกษียณ สมมติว่าเรามีชีวิตอยู่ต่อไปหลังเกษียณแล้วอีก n ปี (ถ้าท่านเกษียณที่อายุ 60 ปี และมีชีวิตอยู่ต่อได้อีก n = 25 ปี นั่นหมายความว่า ท่านคาดการณ์อายุขัยของตนเองไว้เท่ากับ 60 + 25 = 85 ปี) เพื่อให้ครอบคลุมความสนใจของเรา เราก็จะคำนวณ “ผลบวก” ของทุกปี ตั้งแต่ปีที่ 1 ไปจนถึงปีที่ 25 นั่นเอง
[สำหรับท่านที่ไม่คุ้นเคย ซิกมา หรือ Σ เป็นตัวอักษรกรีกที่แปลเป็นภาษาคนง่าย ๆ ว่า “ผลบวก”]
เมื่อคิดผลบวก (ตั้งแต่ปีที่ 1 จนถึงปีที่ n) กับทั้งสองฝั่งของสมการ จะได้
หากลองแทนค่า i = 1, 2, 3,... ไปจนถึง n จะพบว่าฝั่งซ้ายของสมการเท่ากับ Ln – L0 ซึ่งเราออกแบบให้มีการไถ่ถอนหรือสร้างกระแสเงินให้พอดีกับที่จะใช้จ่าย ทำให้ไม่มีการสะสมเงินสดคงค้าง และฝั่งซ้ายนี้ก็จะกลายเป็นศูนย์ ส่วนฝั่งขวาของสมการนั้น พจน์ที่หนึ่ง (ΣP) และพจน์ที่สาม (ΣX) สามารถลดรูปลงได้
จากสมมติฐานที่ว่า Passive Cash Flow ในแต่ละปีมาจาก เงินปันผล ที่สินทรัพย์ A จ่ายออกมาด้วยอัตราผลตอบแทนเงินปันผล (d) ที่ค่อนข้างคงที่ ดังนั้น ΣP = Σ(dA) = d Σ(A) ในกรณีที่สินทรัพย์เป็นพอร์ตโฟลิโอที่ประกอบด้วยหุ้นของบริษัทที่มีธุรกิจอิ่มตัวและจ่ายเงินปันผลอย่างสม่ำเสมอ เราสามารถคาดการณ์การเติบโตในระยะยาวเท่ากับอัตราเงินเฟ้อ ส่วนค่าใช้จ่าย X ก็เติบโตในอัตราเดียวกับอัตราเงินเฟ้อด้วยเช่นกัน
เมื่อเป็นเช่นนี้ จะได้ว่า ΣA = nA1 และ ΣX = nX1 ทำให้สามารถเขียนสมการข้างต้นให้อยู่ในรูป real term ซึ่งตัดผลกระทบจากเงินเฟ้อออกไปได้
ดังนั้น เราจะต้องไถ่ถอนเงินสด (แทะเงินก้อน) ตลอดช่วงเวลาการเกษียณ เท่ากับ
ถ้า X1 = dA1 ฝั่งขวาของสมการจะกลายเป็นศูนย์ หมายความว่า เราไม่ต้องแทะเงินก้อนเลย และในทางตรงข้าม หากเราไม่มีสินทรัพย์ที่สร้างกระแสเงินสดเลย (A1 = 0) ก็จะได้ว่า ΣR = nX1 ซึ่งก็แปลว่า เราต้องเตรียมเงินก้อนเอาไว้เท่ากับค่าใช้จ่ายของปีแรก (X1) คูณด้วยจำนวนปีที่จะอยู่หลังเกษียณ (n) แล้วก็ต้องเอาไปฝากหรือทำอะไรให้มีผลตอบแทนเท่า ๆ กับอัตราเงินเฟ้อด้วย ถึงจะมีเงินพอให้แทะตลอดอายุขัย
การตัดสินใจครั้งสำคัญ
หากท่านต้องเลือกระหว่าง (1) การสร้างพอร์ตลงทุน A1 ที่สร้างกระแสเงินสดเลี้ยงเราไปตลอดชีพ และ (2) การเตรียมเงินก้อน ΣR ที่เพียงพอสำหรับการแทะกินไปได้ตลอดชีวิต นั่นแสดงว่าท่านกำลังเปรียบเทียบระหว่าง X1/d (เพราะว่า X1 = dA1) กับ nX1
ในกรณีที่ท่านสามารถสร้างพอร์ตลงทุนที่ให้ผลตอบแทนเงินปันผล d ที่มีค่ามากกว่า 1/n ได้ การสร้างกระแสเงินสดจะดีกว่าการแทะเงินก้อน
ตัวอย่างเช่น สมมติท่านเตรียมเกษียณที่อายุ 60 ปี และคาดว่าจะมีชีวิตอยู่ต่อไปหลังจากนั้น 25 ปี (n = 25) ด้วยการใช้จ่ายเดือนละ 2 หมื่นบาท การแทะเงินก้อนจะทำให้เงินเก็บ 6 ล้านบาทของท่านหมดไปพอดี เพราะ nX1 = 25 ปี x (20000 บาท x 12 เดือน) = 6,000,000 บาท
ในทางตรงข้าม หากท่านนำเงินจำนวนเดียวกันไปสร้างพอร์ตลงทุนที่ให้ผลตอบแทน d = 1/25 หรือ 4% ต่อปี พอร์ตลงทุนของท่านจะจ่ายเงินปันผลออกมาปีละ 0.04 x 6000000 = 240,000 บาท หรือเทียบเท่าเดือนละ 20,000 บาทพอดีเช่นกัน และเงินปันผลนี้ยังเติบโตเท่ากับอัตราเงินเฟ้อ (สมมติว่า 2 เปอร์เซ็นต์) ทำให้สามารถรองรับค่าใช้จ่าย (ซึ่งก็เพิ่มขึ้นในอัตราเดียวกับเงินเฟ้อด้วยเหมือนกัน) ได้ไปจนตลอดชีวิต
ความแตกต่างก็คือ เมื่อครบเวลา 25 ปีแล้ว การแทะเงินก้อนจะทำให้เงินเก็บ 6 ล้านบาทหมดสิ้นไป แต่พอร์ตลงทุนที่สร้างกระแสเงินสด นอกจากไม่หมดแล้วยังสามารถเติบโตขึ้นเป็น 6000000 x 1.02^25 = 9.84 ล้านบาทได้อีกต่างหาก ถ้าไม่ยกให้ลูกหลานญาติมิตร จะเขียนพินัยกรรมทำบุญส่งท้ายก็เป็นกุศลดี
ความเสี่ยงล่ะ?
ถึงตรงนี้หลายท่านคงเห็นแล้วว่าการสร้างกระแสเงินสดมีความยั่งยืนกว่าการแทะเงินก้อน แต่ก็อาจมีบางท่านกังวลในเรื่องของความเสี่ยง และคิดว่าอย่างน้อยถ้าเก็บเงินก้อนไว้แทะ เงินนั้นก็ยัง "ไม่หาย" จนกว่าเราจะหยิบมันออกมาใช้จ่าย ต่างจากพอร์ตลงทุนซึ่งอาจเจ๊งหมดตัวได้
ความกังวลข้อนี้มีทั้งที่จริงและไม่จริง ประการแรก คือ เงินก้อนที่เก็บไว้แทะก็อาจหายหรือลดน้อยลงได้เหมือนกัน แม้จะเป็นการซื้อกองทุนรวมตราสารหนี้ที่คิดว่ามีความเสี่ยงต่ำ เพราะผู้จัดการกองทุนอาจนำเงินของเราไปซื้อตราสารหนี้เอกชน ซึ่งก็มีความเสี่ยงที่จะผิดนัดชำระหนี้และทำให้เงินต้นหายไปได้ ตัวอย่างนี้มีให้เห็นมาแล้วในช่วงวิกฤติเศรษฐกิจของไทยเราเอง
ตัวอย่างผลขาดทุนจากกองทุนรวมตราสารหนี้ในช่วงวิกฤติเศรษฐกิจ
* ในช่วงเวลาดังกล่าว หลาย ๆ กองทุนประเภทเดียวกันก็มีชะตากรรมแบบนี้ นักลงทุนโปรดเข้าใจว่าเป็นความเสี่ยงตามประเภทของกองทุน *
ไม่เพียงเท่านั้น ในช่วงวิกฤติแม้แต่ธนาคารยังแทบเอาตัวกันไม่รอด เงินฝากธนาคารที่คิดว่าแน่ก็ยังอาจไม่แน่ได้เหมือนกัน หรือถ้าจะได้เงินคืนเต็มจำนวนก็อาจต้องใช้เวลามากขึ้น ส่วนผลตอบแทนก็แทบไม่ต้องพูดถึง
ประการที่สอง พอร์ตลงทุนอาจเจ๊งหมดตัวหรือไม่ก็ได้ ขึ้นอยู่กับ "ไส้ใน" ที่เราจัดไว้ หากพอร์ตลงทุนของเราประกอบด้วยหุ้นหวือหวาเก็งกำไร หุ้นที่มี P/E สูง ๆ เช่น 50-60 เท่า โอกาสที่ราคาหุ้นในพอร์ตจะปรับตัวลงแรง ๆ ก็เป็นไปได้มาก
ในทางกลับกัน หากท่านจัดพอร์ตให้มีหุ้นชั้นนำขนาดใหญ่ที่ผ่านร้อนผ่านหนาวและจ่ายเงินปันผลได้อย่างสม่ำเสมอมาเป็นสิบปี ผสมผสานกับกองทุนอสังหาริมทรัพย์และกองทุนตราสารหนี้ โอกาสที่ท่านจะเจ๊งหรือขาดทุนแรง ๆ ก็มีไม่มาก โดยเฉพาะเมื่อเป็นการลงทุนระยะยาว 20-30 ปี
ประการที่สาม แม้ท่านจะเห็น มูลค่าพอร์ต ลดลงหรือเพิ่มขึ้นตามสภาพตลาด แต่ตราบเท่าที่ "กระแสเงินสด" ยังแข็งแกร่ง ท่านก็ไม่มีเหตุให้วิตก เพราะสิ่งที่ท่านต้องการจริง ๆ คือ กระแสเงินสด ไม่ใช่มูลค่าพอร์ตครับ





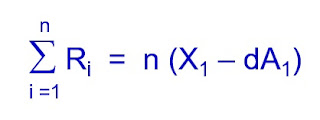


ไม่มีความคิดเห็น:
แสดงความคิดเห็น