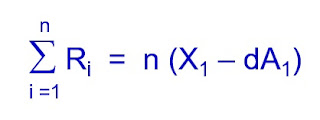ห่วงเงินต้น... จนหมดตัว

ด้วยแนวคิดที่ว่า "เมื่ออายุมากขึ้น คนเราควรลงทุนอย่างอนุรักษนิยมมากขึ้น" พอร์ตลงทุนของคนวัยเกษียณจึงมักถูกออกแบบให้มีความระแวดระวัง โดยพยายามอย่างถึงที่สุดที่จะไม่ให้ขาดทุนหรือสูญเสียเงินต้นเลย แม้ได้ผลตอบแทนน้อยก็ไม่เป็นไร

การลงทุนอย่างระมัดระวังสุด ๆ โดยมุ่งรักษาเงินต้น อาจทำให้คนวัยทำงานรวยช้า แต่กับคนวัยเกษียณ นี่อาจทำให้หมดตัวได้ เหตุผลก็เพราะว่าโดยทั่วไปแล้วคนวัยเกษียณมักจำเป็นต้องดึงเงินบางส่วนออกมาจากพอร์ต เพื่อนำมาเป็นค่าใช้จ่ายในชีวิตประจำวัน (ต่างจากคนวัยทำงานที่มักใช้จ่ายเงินจากรายได้ประจำ แล้วส่วนที่เหลือเก็บจึงค่อยนำมาลงทุน)

เมื่อพอร์ตลงทุนให้ผลตอบแทนน้อยมาก เงินที่ดึงออกมาก็แทบจะเป็นส่วนของเงินต้นล้วน ๆ พอร์ตของเขาจึงหดลง เริ่มจากทีละน้อย และค่อย ๆ เร่งตัวมากขึ้นจนกระทั่งหมดไป

ตัวอย่างพอร์ตลงทุนของผู้เกษียณอายุที่มีค่าใช้จ่ายเดือนละ 20,000 บาท ภายใต้อัตราเงินเฟ้อ 3 เปอร์เซ็นต์ และได้ผลตอบแทน 1.87 เปอร์เซ็นต์ต่อปี เทียบเท่าผลตอบแทนจากพันธบัตรรัฐบาลที่มีอายุ 5 ปี

ทั้งนี้ เส้นตรงสีแดงในภาพกำกับไว้เพื่อให้เห็นชัดเจนขึ้นว่า การหดตัวลงของพอร์ตโฟลิโอมีการเร่งตัวในช่วงท้าย ก่อนที่มูลค่าพอร์ตจะกลายเป็นศูนย์ในระหว่างปีที่ 16 หลังเกษียณ ถ้าอายุเกษียณมาตรฐาน 60 ปี ก็เท่ากับว่ามีเงินใช้จ่ายถึงอายุ 75 ปีกว่า ๆ ใกล้เคียงกับอายุขัยเฉลี่ยของคนไทยตามข้อมูลจากธนาคารโลกพอดี ซึ่งสอดคล้องกับสื่อและแหล่งความรู้ทางการเงินที่แนะนำให้เก็บเงินเพื่อการเกษียณอย่างน้อย 4 ล้านบาท ตามที่เราเคยได้ยินกันมา

อย่างไรก็ตาม ท่านทั้งหลายควรตระหนักด้วยว่า การมีเงินแค่พอใช้ถึงค่าเฉลี่ยอายุขัยนั้นออกจะน่ากลัวเกินไป เพราะถ้าประเมินคร่าว ๆ ว่า ค่าเฉลี่ย อยู่ตรงประมาณกึ่งกลางของประชากรทั้งหมด โอกาสที่ตัวเราจะเป็นหนึ่งในประชากรที่มีอายุขัยยาวนานกว่าตัวเลขนี้ก็จะเท่ากับ 50-50 หรือพอ ๆ กับการโยนเหรียญ

จุดหมดตัว

ถึงตรงนี้หลายท่านน่าจะสังเกตเห็นความแตกต่างระหว่าง การลงทุน กับ การจัดการเงิน ของคนวัยเกษียณ ทั้งสองสิ่งนี้แม้จะมีความสัมพันธ์กัน แต่ก็เป็นคนละส่วนอยู่ดี

สำหรับชีวิตหลังเกษียณ ความมุ่งหมายสำคัญอยู่ที่การ "มีเงินใช้ตลอดชีพ" หาใช่การ "ไม่ขาดทุน" แต่อย่างใด ต่อให้เราลงทุนแล้วไม่เสียเงินเลย แต่การทยอยไถ่ถอนเงินทุนก็ทำให้หมดตัวได้ ณ จุดใดจุดหนึ่งในอนาคต ซึ่งผมขอเรียกว่า จุดหมดตัว ภารกิจของนักลงทุนวัยเกษียณ ได้แก่ การยืดจุดหมดตัวที่ว่านี้ให้ออกไปไกลที่สุด

เพื่อให้เห็นภาพชัดเจนขึ้น ลองมาดูตัวอย่างพอร์ตลงทุนที่แหล่งความรู้อื่น ๆ ไม่กล้าแนะนำกันบ้าง

ตัวอย่างพอร์ตลงทุนของผู้เกษียณอายุที่มีค่าใช้จ่ายเดือนละ 20,000 บาท ภายใต้อัตราเงินเฟ้อ 3 เปอร์เซ็นต์ และลงทุนหุ้นได้ผลตอบแทน 7 เปอร์เซ็นต์ต่อปี แบ่งเป็นการเติบโตของมูลค่าเงินทุน (capital growth) 3 เปอร์เซ็นต์ต่อปี และเงินปันผล 4 เปอร์เซ็นต์ต่อปี

นี่เป็นกรณีที่ค่อนข้างสุดขั้ว เมื่อคนวัยเกษียณนำเงินทั้งหมด 4 ล้านบาทเท่ากันไปลงทุนหุ้นและได้รับผลตอบแทนในระดับปานกลาง (หรืออาจจะค่อนข้างแย่เสียด้วยซ้ำในสายตาของบางท่าน) สังเกตว่า จุดหมดตัว ขยับไปอยู่ที่ปีที่ 29 หลังเกษียณ หรือเทียบเท่าอายุ 89 ปี

พอร์ตลงทุนแบบนี้นับว่า "เสี่ยงมากขึ้น" ในแง่ของการลงทุน เนื่องจากถือครองหุ้นเอาไว้เต็มอัตรา แต่ควรถือว่า "เสี่ยงน้อยลง" ในแง่ของการจัดการเงินในภาพรวม เพราะจุดหมดตัวอยู่ห่างออกไปมาก แม้จะยังคงกินอยู่และใช้จ่ายเท่าเดิม

ข้อสังเกตประการหนึ่งของพอร์ตสุดขั้วนี้ คือ ขนาดของพอร์ตมีการเติบโตขึ้นในช่วงแรก ก่อนจะลดลงในภายหลังด้วยอัตราเร่ง เหตุผลก็เพราะว่าผลตอบแทนรวมของพอร์ต 7 เปอร์เซ็นต์ เมื่อหักด้วยค่าใช้จ่ายปีละ 240,000 บาท ซึ่งคิดเป็น 6 เปอร์เซ็นต์ของมูลค่าพอร์ตตั้งต้น จะเท่ากับว่าขนาดของพอร์ตเติบโตได้เพียง 1 เปอร์เซ็นต์ต่อปี (ในช่วงแรก) ช้ากว่าค่าใช้จ่ายซึ่งเติบโตด้วยอัตราเงินเฟ้อ 3 เปอร์เซ็นต์ สุดท้ายจึงโดนค่าใช้จ่ายไล่กวดและต้องไถ่ถอนเงินต้นออกมามากขึ้นเรื่อย ๆ จนกระทั่งหมดตัวไปในที่สุด

หากต้องการมั่นใจว่าจะไม่หมดตัว ท่านจำเป็นต้องยืดจุดหมดตัวออกไปที่อินฟินิตี้ (infinity - ไม่มีที่สิ้นสุด) พูดง่าย ๆ ก็คือ สามารถมีกินมีใช้ตลอดชีวิต เหมือนที่เคยอธิบายไปในบทความชื่อ "แทะเงินก้อน" ซึ่งเหตุการณ์นี้จะเกิดขึ้นได้ ผลตอบแทนรวมของพอร์ตจะต้องเพิ่มขึ้นจาก 7 เปอร์เซ็นต์ เป็น 9 เปอร์เซ็นต์ สอดคล้องกับ สมการอิสรภาพทางการเงิน ที่เคยนำเสนอไปเมื่อ 6-7 ปีที่แล้ว

[ท่านทั้งหลายอาจอัศจรรย์ใจนิดหน่อย เมื่อองค์ความรู้ที่ค้นพบต่างกรรมต่างวาระ สุดท้ายก็กลับมาสอดคล้องกันเองราวกับจิ๊กซอว์ที่อยู่ในชุดเดียวกัน]

จัดพอร์ตให้เหมาะสม

ในกรณีที่ไม่สามารถยืด จุดหมดตัว ออกไปที่อินฟินิตี้ ท่านจำต้องยอมรับความจริงและจัดพอร์ตลงทุนให้เหมาะสม แน่นอนว่าท่านไม่ควรเอาเงินไปฝากธนาคารหรือซื้อกองทุนตราสารหนี้จนหมด ขณะเดียวกันการจัดพอร์ตสุดขั้วโดยลงทุนหุ้น 100 เปอร์เซ็นต์เหมือนในตัวอย่างข้างต้นก็ไม่น่าจะเป็นความคิดที่ดีนัก

ลองมาพิจารณาภาพด้านล่างนี้กัน

หากแบ่งช่วงเวลาหลังเกษียณออกเป็นช่วง ๆ ด้วยสูตรจำนวนปี "ยกกำลังสอง" เหมือนในรูป เราอาจประเมินว่าช่วงเวลาที่ใกล้จะมาถึง (เช่น 2 ปีแรก) เป็นช่วงที่ควรเตรียมเงินสดพร้อมใช้ รูปแบบของสินทรัพย์ที่เหมาะสมกับเงินก้อนนี้ ได้แก่ เงินฝากธนาคาร หรือกองทุนตราสารเงิน ซึ่งสามารถไถ่ถอนได้ภายใน 1-2 วัน โดยไม่ลดมูลค่า

เงินก้อนสำหรับช่วงเวลา 4 ปีถัดไป (เช่น ปีที่ 2 ถึงปีที่ 6) สามารถเลือกลงทุนในสินทรัพย์ที่สร้างผลตอบแทนสูงขึ้นและมีความผันผวนไม่มาก เช่น กองทุนตราสารหนี้ระยะสั้นหรือระยะกลาง ส่วนสินทรัพย์ที่เหมาะสำหรับค่าใช้จ่ายในช่วงปีที่ 6 ถึงปีที่ 14 อาจเน้นไปที่การสร้างกระแสเงินสดและการเติบโตมากขึ้น เช่น กองทุนรวมที่กระจายลงทุนในกองรีท (REIT) หรือกองทุนรวมอสังหาริมทรัพย์หลาย ๆ กอง หรือแม้แต่กองทุนรวมหุ้นที่เน้นหุ้นปันผลดี

ในส่วนของสินทรัพย์ที่จะรองรับค่าใช้จ่ายช่วงปีที่ 14 ถึงปีที่ 30 เราน่าจะสามารถสร้างผลตอบแทนและเอาชนะเงินเฟ้อได้ด้วยการลงทุนหุ้นอย่างเต็มที่ เนื่องจากเป็นการลงทุนระยะยาวและกว่าจะต้องใช้เงินก้อนนี้ก็ยังอีก 14 ปีข้างหน้า หากเศรษฐกิจเกิดชะงักงัน อย่างน้อยก็มีเวลานับทศวรรษให้ตลาดหุ้นฟื้นตัว สิ่งสำคัญก็คือ อย่าลืมกระจายการลงทุนไปในหุ้นหลาย ๆ ตัว เพราะ "ตลาดหุ้น" ในภาพรวมมักฟื้นได้หลังวิกฤติ แต่กับ "หุ้นหนึ่งตัว" นั้นไม่แน่

เมื่อพิจารณาดังนี้แล้ว สมมติว่าเรามีเงินเกษียณ 4 ล้านบาท และเตรียมค่าใช้จ่ายไว้ปีละ 240,000 บาท เงินสำหรับสองปีแรกจะเท่ากับ 240000 x 2 = 480,000 บาท ตีง่าย ๆ ว่าก้อนนี้เอาไปฝากธนาคาร

[เพื่อไม่ให้ซับซ้อนมากนัก เราจะตัดเรื่องเงินเฟ้อออกไป แต่ท่านทั้งหลายไม่ต้องกังวล เพราะการลงทุนในภาพรวมของเราให้ผลตอบแทนที่น่าจะพอสู้กับเงินเฟ้อได้อยู่แล้ว]

เงินสำหรับสี่ปีถัดมา 240000 x 4 = 960,000 บาท เอาไปซื้อกองทุนรวมตราสารหนี้

เงินสำหรับแปดปีต่อไป 240000 x 8 = 1,920,000 บาท เอาไปซื้อกองทุนรวมที่ลงทุนในกองอสังหาฯ และกองทุนรวมที่เน้นหุ้นปันผลดี อย่างละเท่า ๆ กัน

เงินส่วนที่เหลือจะเท่ากับ 4000000 - 480000 - 960000 - 1920000 = 640,000 บาท ส่วนนี้เป็นเงินที่เตรียมไว้ใช้จ่ายตั้งแต่ปีที่ 14 เป็นต้นไป จึงเอาไปซื้อกองทุนหุ้น

สรุปตัวอย่างพอร์ตตั้งต้น

*** ข้อสรุปนี้เกิดจากตัวเลขและสมมติฐานข้างต้น เพื่อประโยชน์ในการนำเสนอแนวคิดเท่านั้น ***

นี่เป็นตัวอย่างการจัดพอร์ตลงทุนให้สอดคล้องกับระยะเวลาที่เหลืออยู่ของชีวิตคนวัยเกษียณ ซึ่งมีข้อสังเกตอยู่ 3-4 ประการ

ประการแรก พอร์ตดังกล่าวนี้เป็นเพียง "พอร์ตตั้งต้น" ซึ่งแน่นอนว่าเมื่อเวลาผ่านไป เราก็จะต้องปรับส่วนผสมในพอร์ตเป็นระยะ โดยอาจย้อนกลับไปยังแถบสีที่แบ่งช่วงปีอีกครั้งหนึ่ง แล้วแบ่งสรรสินทรัพย์ไปตามหมวดหมู่เสียใหม่ทุกปีหรือทุกสองปี

ประการที่สอง พอร์ตลงทุนนี้มี จุดหมดตัว ณ ต้นปีที่ 19 หลังเกษียณ เทียบกับกรณีลงทุนอย่างระมัดระวังสุด ๆ [ภาพแรกของบทความ] ซึ่งมีจุดหมดตัวอยู่ประมาณกลางปีที่ 16 การยืดจุดหมดตัวออกไปได้เกือบสามปีนับว่ามีคุณค่าอย่างยิ่งสำหรับคนวัยเกษียณที่กำลังหลังพิงฝา

ประการที่สาม ท่านสามารถใช้แถบสีจำนวนปีรูปแบบอื่น เช่น แทนที่จะกำหนดช่วงแบบยกกำลังสอง (2-4-8-16 ปี) ท่านอาจใช้ตัวเลขง่าย ๆ อย่างเช่น 5-10-15 ปี ก็ได้ โดยหลักแล้วเราจะไม่มีปัญหากับตัวเลขที่แตกต่างกัน ตราบเท่าที่มันสะท้อนแนวคิดเรื่องการลงทุนระยะสั้น-ระยะยาว

ประการที่สี่ สัดส่วนการถือครองหุ้นในระดับ 40 เปอร์เซ็นต์ อาจทำให้กูรูหลายท่านไม่พอใจนัก เพราะพวกเขาคุ้นเคยและมักให้คำแนะนำประเภทบอกต่อกันมา เช่น "คนวัยเกษียณควรถือครองหุ้น 5 เปอร์เซ็นต์ และถือตราสารหนี้กับเงินฝากธนาคารในสัดส่วนที่มาก" แบบนี้ท่านควรถามเขาด้วยว่า "ตัวเลข 5 เปอร์เซ็นต์มาจากไหน?" บางทีท่านอาจจะประหลาดใจที่แม้แต่กูรูเองก็คอนเฟิร์มคำแนะนำของตัวเองไม่ได้ และอาจหงุดหงิดกับคำถามของท่านด้วยซ้ำไป

ส่วนพอร์ตตัวอย่างของเรา เราได้เห็นกันแล้วว่าตัวเลข 40 เปอร์เซ็นต์ มีที่มาอย่างไร และถ้าท่านใส่สมมติฐานใหม่ตามสถานการณ์ของตนเองเข้าไปในโมเดล ตัวเลขใหม่ที่ได้ก็จะถือว่ามีที่มาเช่นกัน ซึ่งท่านสามารถมั่นใจได้มากกว่าคำแนะนำแบบกำปั้นทุบดินที่ฟังต่อกันมา นอกจากนั้นพอเวลาผ่านไป สัดส่วนการลงทุนหุ้นจะลดลงจนเหลือศูนย์ไปเอง หากมีการปรับพอร์ตอย่างสม่ำเสมอตามที่บอกไปข้างต้น นี่เป็นกลไกที่เกิดขึ้นเพื่อผสานแนวคิดเรื่อง การลงทุน และ การจัดการเงิน เข้าด้วยกัน

สำหรับประเด็นเรื่องความเสี่ยงและสัดส่วนการถือครองหุ้นนี้ ไว้ผมจะพยายามหาโอกาสอธิบายเพิ่มเติมในแฟนเพจเฟซบุ๊ก MonkeyFreeTime ต่อไป

แทะเงินก้อน

เป็นที่เชื่อกันโดยทั่วไปว่าเราจำเป็นต้องมีเงินก้อนใหญ่ เพื่อเอาไว้แทะกินหลังเกษียณ บางกระแสระบุว่าจำนวนเงินขั้นต่ำ คือ 4 ล้านบาท แต่ถ้าอยากให้ชีวิตมีคุณภาพ ก็อาจต้องมีถึง 10 ล้านบาท โดย “ดีไซน์” ของการเกษียณในรูปแบบนี้อยู่ตรงที่การทยอยใช้เงินก้อนดังกล่าว และหวังว่าจะไม่หมดเงินก่อนหมดลม

เคยได้ยินไหมครับ ที่เขาบอกว่า “สุดเสียดาย ตายไปยังใช้เงินไม่หมด” กับ “สุดสลด ใช้เงินจนหมดแล้วยังไม่ตาย”

คำถามที่เกิดขึ้นในใจของผม คือ ชีวิตของเราควรจะลุ้นขนาดนั้นเชียวหรือ? และหากมีถึง 10 ล้านบาทจริง เรายังจำเป็นต้องนั่งแทะเงินด้วยใจตุ๊ม ๆ ต่อม ๆ อีกไหม หรือที่จริงเราสามารถเอาเงินก้อนที่ว่ามาสร้างกระแสเงินสดไว้เลี้ยงตัวได้ตลอดชีพสบาย ๆ... และจุดแบ่ง (ว่าจะแทะหรือไม่แทะ) มันอยู่ตรงไหน?

โมเดลการเลี้ยงชีพ

เพื่อตอบคำถามข้างต้น ผมได้สร้างโมเดลที่จะค้นหาความจริง โดยกำหนดให้ชาวเกษียณมีรายได้สองทาง ได้แก่

1. กระแสเงินสดที่ไม่ต้องออกแรงทำงาน (Passive Cash Flow หรือ P) และ


2. เงินที่ทยอยไถ่ถอนมาจากเงินก้อน (Cash Redemption หรือ R)

เมื่อนำรายได้ข้างต้นหัก ค่าใช้จ่าย (Expense หรือ X) เรียบร้อยแล้ว หากมีเงินสดเหลือ เราจะเรียกว่า Cash Leftover หรือ L ซึ่งทั้งหมดจะสามารถเขียนเป็นสมการการใช้เงินของชาวเกษียณในปีที่ 1 ได้ดังนี้

สังเกตว่าในสมการ เราคำนึงถึงเงินสดที่เหลือมาจากปีก่อนหน้า (ปีที่ศูนย์) หรือ L0 ด้วย

จากแนวคิดนี้ เราสามารถเขียนสมการให้อยู่ใน รูปทั่วไป ก็ได้ โดยตัวเลข 1 ที่ห้อยไว้เพื่อแสดงว่าเป็นปีที่ 1 ก็จะเปลี่ยนเป็น i และท่านก็จะสามารถแทนค่า i ให้เป็นตัวเลขปีใด ๆ ที่ท่านต้องการ

เมื่อย้ายข้างจัดรูปเสียหน่อยก็จะได้

หากสังเกตให้ดี ฝั่งขวาของสมการเป็นกระแสเงินสดที่ไหลเข้าและไหลออกในปีนั้น ๆ ส่วนฝั่งซ้ายก็เป็นการสรุปว่าเงินสดที่คงค้างอยู่ในระบบมีการเปลี่ยนแปลงไปเท่าไร

ภาพรวมหลังเกษียณ

แน่นอนว่าความสนใจของเรา ไม่ใช่ ชีวิตหลังเกษียณปีใดปีหนึ่ง แต่เป็นภาพรวมของทุก ๆ ปีภายหลังเกษียณ สมมติว่าเรามีชีวิตอยู่ต่อไปหลังเกษียณแล้วอีก n ปี (ถ้าท่านเกษียณที่อายุ 60 ปี และมีชีวิตอยู่ต่อได้อีก n = 25 ปี นั่นหมายความว่า ท่านคาดการณ์อายุขัยของตนเองไว้เท่ากับ 60 + 25 = 85 ปี) เพื่อให้ครอบคลุมความสนใจของเรา เราก็จะคำนวณ “ผลบวก” ของทุกปี ตั้งแต่ปีที่ 1 ไปจนถึงปีที่ 25 นั่นเอง

[สำหรับท่านที่ไม่คุ้นเคย ซิกมา หรือ Σ เป็นตัวอักษรกรีกที่แปลเป็นภาษาคนง่าย ๆ ว่า “ผลบวก”]

เมื่อคิดผลบวก (ตั้งแต่ปีที่ 1 จนถึงปีที่ n) กับทั้งสองฝั่งของสมการ จะได้

หากลองแทนค่า i = 1, 2, 3,... ไปจนถึง n จะพบว่าฝั่งซ้ายของสมการเท่ากับ Ln – L0 ซึ่งเราออกแบบให้มีการไถ่ถอนหรือสร้างกระแสเงินให้พอดีกับที่จะใช้จ่าย ทำให้ไม่มีการสะสมเงินสดคงค้าง และฝั่งซ้ายนี้ก็จะกลายเป็นศูนย์ ส่วนฝั่งขวาของสมการนั้น พจน์ที่หนึ่ง (ΣP) และพจน์ที่สาม (ΣX) สามารถลดรูปลงได้

จากสมมติฐานที่ว่า Passive Cash Flow ในแต่ละปีมาจาก เงินปันผล ที่สินทรัพย์ A จ่ายออกมาด้วยอัตราผลตอบแทนเงินปันผล (d) ที่ค่อนข้างคงที่ ดังนั้น ΣP = Σ(dA) = d Σ(A) ในกรณีที่สินทรัพย์เป็นพอร์ตโฟลิโอที่ประกอบด้วยหุ้นของบริษัทที่มีธุรกิจอิ่มตัวและจ่ายเงินปันผลอย่างสม่ำเสมอ เราสามารถคาดการณ์การเติบโตในระยะยาวเท่ากับอัตราเงินเฟ้อ ส่วนค่าใช้จ่าย X ก็เติบโตในอัตราเดียวกับอัตราเงินเฟ้อด้วยเช่นกัน

เมื่อเป็นเช่นนี้ จะได้ว่า ΣA = nA1 และ ΣX = nX1 ทำให้สามารถเขียนสมการข้างต้นให้อยู่ในรูป real term ซึ่งตัดผลกระทบจากเงินเฟ้อออกไปได้

ดังนั้น เราจะต้องไถ่ถอนเงินสด (แทะเงินก้อน) ตลอดช่วงเวลาการเกษียณ เท่ากับ

ถ้า X1 = dA1 ฝั่งขวาของสมการจะกลายเป็นศูนย์ หมายความว่า เราไม่ต้องแทะเงินก้อนเลย และในทางตรงข้าม หากเราไม่มีสินทรัพย์ที่สร้างกระแสเงินสดเลย (A1 = 0) ก็จะได้ว่า ΣR = nX1 ซึ่งก็แปลว่า เราต้องเตรียมเงินก้อนเอาไว้เท่ากับค่าใช้จ่ายของปีแรก (X1) คูณด้วยจำนวนปีที่จะอยู่หลังเกษียณ (n) แล้วก็ต้องเอาไปฝากหรือทำอะไรให้มีผลตอบแทนเท่า ๆ กับอัตราเงินเฟ้อด้วย ถึงจะมีเงินพอให้แทะตลอดอายุขัย

การตัดสินใจครั้งสำคัญ

หากท่านต้องเลือกระหว่าง (1) การสร้างพอร์ตลงทุน A1 ที่สร้างกระแสเงินสดเลี้ยงเราไปตลอดชีพ และ (2) การเตรียมเงินก้อน ΣR ที่เพียงพอสำหรับการแทะกินไปได้ตลอดชีวิต นั่นแสดงว่าท่านกำลังเปรียบเทียบระหว่าง X1/d (เพราะว่า X1 = dA1) กับ nX1

ในกรณีที่ท่านสามารถสร้างพอร์ตลงทุนที่ให้ผลตอบแทนเงินปันผล d ที่มีค่ามากกว่า 1/n ได้ การสร้างกระแสเงินสดจะดีกว่าการแทะเงินก้อน

ตัวอย่างเช่น สมมติท่านเตรียมเกษียณที่อายุ 60 ปี และคาดว่าจะมีชีวิตอยู่ต่อไปหลังจากนั้น 25 ปี (n = 25) ด้วยการใช้จ่ายเดือนละ 2 หมื่นบาท การแทะเงินก้อนจะทำให้เงินเก็บ 6 ล้านบาทของท่านหมดไปพอดี เพราะ nX1 = 25 ปี x (20000 บาท x 12 เดือน) = 6,000,000 บาท

ในทางตรงข้าม หากท่านนำเงินจำนวนเดียวกันไปสร้างพอร์ตลงทุนที่ให้ผลตอบแทน d = 1/25 หรือ 4% ต่อปี พอร์ตลงทุนของท่านจะจ่ายเงินปันผลออกมาปีละ 0.04 x 6000000 = 240,000 บาท หรือเทียบเท่าเดือนละ 20,000 บาทพอดีเช่นกัน และเงินปันผลนี้ยังเติบโตเท่ากับอัตราเงินเฟ้อ (สมมติว่า 2 เปอร์เซ็นต์) ทำให้สามารถรองรับค่าใช้จ่าย (ซึ่งก็เพิ่มขึ้นในอัตราเดียวกับเงินเฟ้อด้วยเหมือนกัน) ได้ไปจนตลอดชีวิต

ความแตกต่างก็คือ เมื่อครบเวลา 25 ปีแล้ว การแทะเงินก้อนจะทำให้เงินเก็บ 6 ล้านบาทหมดสิ้นไป แต่พอร์ตลงทุนที่สร้างกระแสเงินสด นอกจากไม่หมดแล้วยังสามารถเติบโตขึ้นเป็น 6000000 x 1.02^25 = 9.84 ล้านบาทได้อีกต่างหาก ถ้าไม่ยกให้ลูกหลานญาติมิตร จะเขียนพินัยกรรมทำบุญส่งท้ายก็เป็นกุศลดี

ความเสี่ยงล่ะ?

ถึงตรงนี้หลายท่านคงเห็นแล้วว่าการสร้างกระแสเงินสดมีความยั่งยืนกว่าการแทะเงินก้อน แต่ก็อาจมีบางท่านกังวลในเรื่องของความเสี่ยง และคิดว่าอย่างน้อยถ้าเก็บเงินก้อนไว้แทะ เงินนั้นก็ยัง "ไม่หาย" จนกว่าเราจะหยิบมันออกมาใช้จ่าย ต่างจากพอร์ตลงทุนซึ่งอาจเจ๊งหมดตัวได้

ความกังวลข้อนี้มีทั้งที่จริงและไม่จริง ประการแรก คือ เงินก้อนที่เก็บไว้แทะก็อาจหายหรือลดน้อยลงได้เหมือนกัน แม้จะเป็นการซื้อกองทุนรวมตราสารหนี้ที่คิดว่ามีความเสี่ยงต่ำ เพราะผู้จัดการกองทุนอาจนำเงินของเราไปซื้อตราสารหนี้เอกชน ซึ่งก็มีความเสี่ยงที่จะผิดนัดชำระหนี้และทำให้เงินต้นหายไปได้ ตัวอย่างนี้มีให้เห็นมาแล้วในช่วงวิกฤติเศรษฐกิจของไทยเราเอง

   ตัวอย่างผลขาดทุนจากกองทุนรวมตราสารหนี้ในช่วงวิกฤติเศรษฐกิจ

   * ในช่วงเวลาดังกล่าว หลาย ๆ กองทุนประเภทเดียวกันก็มีชะตากรรมแบบนี้ นักลงทุนโปรดเข้าใจว่าเป็นความเสี่ยงตามประเภทของกองทุน *

ไม่เพียงเท่านั้น ในช่วงวิกฤติแม้แต่ธนาคารยังแทบเอาตัวกันไม่รอด เงินฝากธนาคารที่คิดว่าแน่ก็ยังอาจไม่แน่ได้เหมือนกัน หรือถ้าจะได้เงินคืนเต็มจำนวนก็อาจต้องใช้เวลามากขึ้น ส่วนผลตอบแทนก็แทบไม่ต้องพูดถึง

ประการที่สอง พอร์ตลงทุนอาจเจ๊งหมดตัวหรือไม่ก็ได้ ขึ้นอยู่กับ "ไส้ใน" ที่เราจัดไว้ หากพอร์ตลงทุนของเราประกอบด้วยหุ้นหวือหวาเก็งกำไร หุ้นที่มี P/E สูง ๆ เช่น 50-60 เท่า โอกาสที่ราคาหุ้นในพอร์ตจะปรับตัวลงแรง ๆ ก็เป็นไปได้มาก

ในทางกลับกัน หากท่านจัดพอร์ตให้มีหุ้นชั้นนำขนาดใหญ่ที่ผ่านร้อนผ่านหนาวและจ่ายเงินปันผลได้อย่างสม่ำเสมอมาเป็นสิบปี ผสมผสานกับกองทุนอสังหาริมทรัพย์และกองทุนตราสารหนี้ โอกาสที่ท่านจะเจ๊งหรือขาดทุนแรง ๆ ก็มีไม่มาก โดยเฉพาะเมื่อเป็นการลงทุนระยะยาว 20-30 ปี

ประการที่สาม แม้ท่านจะเห็น มูลค่าพอร์ต ลดลงหรือเพิ่มขึ้นตามสภาพตลาด แต่ตราบเท่าที่ "กระแสเงินสด" ยังแข็งแกร่ง ท่านก็ไม่มีเหตุให้วิตก เพราะสิ่งที่ท่านต้องการจริง ๆ คือ กระแสเงินสด ไม่ใช่มูลค่าพอร์ตครับ