มูลค่าของกองทุนที่มีอายุจำกัด

หลักสมมติอันหนึ่งที่แทรกอยู่ในทุกการประเมินมูลค่าหุ้น คือ บริษัทจะเปิดดำเนินกิจการ “ไปชั่วนิรันดร์” (Going Concern Basis) ด้วยเหตุนี้ สูตรคำนวณมูลค่าหุ้นทั่วไปจึง ไม่ สามารถใช้ได้กับกองรีท, กองอสังหาฯ หรือกองทุนรวมโครงสร้างพื้นฐานที่มีอายุจำกัด เช่น 20 ปี หรือ 30 ปี

เพื่อความชัดเจน เราจะแสดงตัวอย่างการประเมินมูลค่าจากกระแสเงินสดสำหรับ หุ้นทั่วไป เสียก่อน จากนั้นค่อยแสดงให้เห็นว่าควรดัดแปลงอย่างไรให้เหมาะสมกับบรรดา กองทุน/กองรีท ที่มีอายุจำกัด ซึ่งความรู้นี้จะช่วยเพิ่มโอกาสชนะให้กับท่านนักลงทุนได้

เริ่มจากเบสิก

สมมติเราประเมินมูลค่าหุ้นด้วยโมเดลการเติบโตคงที่ โดยในปีแรกหุ้นสร้างกระแสเงินสด (เงินปันผล) D₁ และมีอัตราการเติบโตคงที่ g ไปชั่วนิรันดร์ ผู้ถือหุ้นที่ต้องการผลตอบแทน r จะสามารถคำนวณมูลค่าหุ้นได้จากโมเดลการเติบโตของกอร์ดอน (Gordon Growth Model) แบบตรงไปตรงมา

ในการข้ามไปสู่กรณีกองทุนจำกัดอายุ ท่านนักลงทุนอาจใช้สมมติฐานการเติบโตคงที่ต่อยอดไปจากโมเดลนี้ โดยระบุปีที่สิ้นสุดกองทุน (ปีที่ n) กำกับไว้

สังเกตว่าหากคำนวณหา “มูลค่าเฉพาะส่วนที่เป็นแท่งสีฟ้าอ่อน” แล้วหักออกไปจากมูลค่าทั้งหมดได้ เราก็จะเหลือเฉพาะแท่งสีน้ำเงิน กลายเป็นมูลค่าของกองทุนจำกัดอายุพวกนี้นั่นเอง

ต่อยอดด้วยจินตนาการ

ในการทำเช่นนั้น ก่อนอื่นเราต้องย้ายตัวเรา (ที่เป็นหน้ายิ้มหัวกลม ๆ) เข้าไปยืนอยู่ตรงปีที่ n

เมื่อเงยขึ้นไปข้างหน้าหนึ่งปี เราก็หาว่ากระแสเงินสด (แท่งที่เป็นลาย) มีค่าเท่าไร ซึ่งที่จริงก็หาไม่ยาก เพราะมันคือกระแสเงินสดปีแรก (D₁) ที่เติบโตต่อเนื่องขึ้นมาอีกเป็นจำนวน n ปี กลายเป็น D₁ (1 + g)ⁿ

พอรู้ค่านี้แล้ว เราก็พร้อมประเมินเหล่าแท่งสีฟ้าตามแบบฉบับ Gordon Growth Model โดยนำกระแสเงินสดปีถัดไป D₁ (1 + g)ⁿ มาหารด้วย (r - g)

เมื่อทราบมูลค่าเหล่าแท่งสีฟ้า “ณ ปีที่ n” แล้ว มันก็ไม่ยากที่จะคิดลด (discount) กลับมาเป็นมูลค่าในปัจจุบัน

พอจัดรูปแล้ว เราอาจมองผลลัพธ์นี้เป็น สูตรกอร์ดอน (พจน์แรก - สีน้ำเงิน) ที่ปรับค่าตามจำนวนปี n ที่ยืดออกไป สังเกตว่าหากไม่มีการยืดเวลาออกไปเลย (n = 0) จะทำให้พจน์หลัง (สีม่วง) มีค่าเป็นหนึ่ง [เนื่องจากตัวเลขใด ๆ ยกกำลังศูนย์มีค่าเท่ากับหนึ่ง] ผลลัพธ์รวมจึงกลายเป็นสูตรกอร์ดอนตามปกตินั่นเอง

สูตรประเมินมูลค่า

ดังที่กล่าวไปแต่ต้นว่า มูลค่าของกองทุนจำกัดอายุ เท่ากับ มูลค่าของกองทุนไม่จำกัดอายุ ลบด้วย “มูลค่าเฉพาะส่วนที่เป็นแท่งสีฟ้าอ่อน” ดังนั้น

ทั้งนี้ จะขอยกตัวอย่างการประเมินกองทุนรวมโครงสร้างพื้นฐานด้านคมนาคมกองหนึ่ง เพื่อให้เข้าใจการสูตรนำไปใช้นะครับ

สมมติกองทุนดังกล่าวมีอายุคงเหลือ n = 22 ปี โดยคาดว่าเงินปันผลปีถัดไป D₁ = 0.48 บาท ซึ่งน่าจะเติบโตในอัตราต่อเนื่องระยะยาว g = 1.5% และนักลงทุนต้องการผลตอบแทน r = 5%

เมื่อแทนค่าตามสมมติฐานข้างต้นเข้าไปในสูตร จะได้มูลค่าหน่วยลงทุนเท่ากับ 7.21 บาท เทียบกับราคาตลาดปัจจุบัน 7.15 บาท นักลงทุนจึงอาจพิจารณาซื้อกองทุนนี้ได้ หากมีสมมติฐานดังที่กล่าวมาและยอมรับผลตอบแทนในระดับราว ๆ 5 เปอร์เซ็นต์ต่อปี

ถึงตรงนี้ทุกท่านก็ได้เห็นแล้วว่าเราจะดัดแปลงสูตรการประเมินมูลค่าหุ้นให้ใช้งานได้กับ กองทุน/กองรีท ที่มีอายุจำกัด และนำไปใช้งานจริงได้อย่างไร ก็หวังว่าจะเป็นประโยชน์สำหรับการลงทุนครับ

หุ้นถูก... หรือ หุ้นน่าซื้อ?

หิว กับ อยากกิน นั้นไม่เหมือนกัน บางครั้งเราอยากกินทั้งที่ไม่หิว หรือบางทีหิว แต่เจออาหารแย่ก็ไม่อยากกิน

ในเชิงของหุ้น หุ้นถูก กับ หุ้นน่าซื้อ เองก็มีความแตกต่างกัน ซึ่งบทความนี้จะพาท่านไปพบความจริงที่น่าตื่นตะลึง แถมยังแทรกความน่าขันและน่าปวดใจไปพร้อม ๆ กัน

ความเป็นไปได้ทั้ง 4

โดยธรรมชาตินักลงทุนจะ “รู้สึก” ถึงความถูกแพงของหุ้นแตกต่างกันไปตามช่วงเวลา ถ้าหุ้นเคยป้วนเปี้ยนอยู่แถว ๆ 10 บาท แล้วต่อมาราคาพุ่งขึ้นไปที่ 13-14 บาท นักลงทุนก็จะเริ่มรู้สึกว่าหุ้นแพง หรือในทางกลับกัน หากหุ้นปรับตัวลงไปที่ 6 บาท พวกเขาก็อาจรู้สึกว่าหุ้นถูกมากแล้ว

แต่แน่ล่ะ หุ้นถูกอาจจะน่าซื้อหรือไม่น่าซื้อก็ได้ กรณีข้างต้นถ้านักลงทุนเชื่อว่าราคาหุ้นมีโอกาสปรับตัวลงไปอีก เช่น จาก 6 บาท แล้วยังลงไปต่ำกว่า 5 บาทได้ แบบนี้แม้หุ้นมีราคาเพียง 6 บาท ก็ไม่เรียกว่าน่าซื้อ

ดังนั้น เราสามารถจำแนกสถานการณ์ทั้ง 4 แบบในรูปตาราง โดยกำกับความคิดเห็นลงไปด้วย

 

ตัวอย่างของหุ้นถูกและน่าซื้อ คือ ราคาหุ้นลดลงมาต่ำ และมีปัจจัยเกื้อหนุนต่อการฟื้นตัว ซื้อแล้วน่าจะ ปลอดภัย แต่กลับกันถ้าราคาหุ้นลงมาเยอะแล้ว และมีโอกาสลงต่อยาว ๆ อันนี้เรียกว่า หุ้นถูกแต่ไม่น่าซื้อ แบบนี้ทางออกอาจเป็นการ ปล่อยไป ไม่เข้าไปยุ่ง

ในทางตรงข้าม สถานการณ์ที่หุ้นแพงทว่ายังคงน่าซื้อ เกิดขึ้นเมื่อราคาหุ้นปรับตัวขึ้นมาเยอะโดยมีเหตุผลที่ดีรองรับ ถ้าใจกล้าซื้อไว้ก็อาจจะ คุ้มเสี่ยง แต่หากตรงข้าม คือ หุ้นพุ่งขึ้นมาเยอะเกินตัว แล้วเหตุผลรองรับที่จับต้องได้ก็ไม่มีเพียงพอ อย่างนี้จะเป็นสถานการณ์ที่หุ้นแพงแถมยังไม่น่าซื้อด้วย คงต้องรอให้ คนบ้า มาซื้อไป

เมื่อทราบความเป็นไปได้ทั้ง 4 แบบแล้ว ส่วนใหญ่คนที่มีเหตุมีผลและระแวดระวังจะเลือกซื้อหุ้นในช่องซ้ายบน (วิถีปลอดภัย) หรือถ้าใจกล้าหน่อยก็อาจจะเลือกช่องซ้ายล่าง (ซื้อแพง เพื่อไปขายแพงกว่า)

พูดง่าย ๆ คือ นักลงทุนที่มีเหตุผลมักซื้อ เมื่อหุ้นน่าซื้อ นั่นเอง

สร้างโมเดล

เพื่อให้เข้าใจกระบวนการลงทุนมากขึ้น เราจะสร้างโมเดลการเคลื่อนไหวของ ราคาหุ้น ในลักษณะวัฏจักรอย่างง่ายที่มีวงรอบประมาณ 4 ปี แสดงด้วยเส้นสีฟ้า

หากเราพิจารณาว่าหุ้นเกือบทุกตัวล้วนมีความเป็นวัฏจักรเกี่ยวพันกับสภาพเศรษฐกิจโดยรวมอยู่ไม่มากก็น้อย โมเดลอย่างง่ายนี้ย่อมทำให้ท่านเห็นความเป็นไปและมีประโยชน์อยู่บ้าง มากน้อยตามแต่คุณลักษณะของหุ้นที่ท่านสนใจ

สมมติว่ามีการประเมิน มูลค่าหุ้น หรือราคาเป้าหมาย เป็นเส้นประสีส้ม เส้นประนี้ควรวิ่งล้อไปกับราคาหุ้น แต่ “ล้าหลัง” อยู่เล็กน้อย

เหตุที่เป็นเช่นนี้ก็เพราะว่าการคาดการณ์ไปในอนาคต (เพื่อประเมินมูลค่าหุ้น) นั้น อาศัยมุมมองของนักวิเคราะห์หรือนักลงทุน และมุมมองดังกล่าวก็ประมวลขึ้นจากสิ่งที่เกิดขึ้นในอดีต การประเมินมูลค่าหุ้นจึงแฝงองค์ประกอบที่มีความล้าหลังไปด้วยอย่างไม่อาจหลีกเลี่ยงได้

นอกจากเรื่องของการล้าหลังแล้ว อีกข้อหนึ่งที่ควรสังเกต คือ มุมมองของนักวิเคราะห์มักดีเกินจริงในช่วงเวลาที่ดี และมักแย่เกินจริงในช่วงเวลาที่แย่ สะท้อนด้วยมูลค่าหุ้นที่พุ่งขึ้นหรือลดลงทะลุระดับราคาที่หุ้นไปถึงจริง ข้อนี้เกิดจากความไม่สมบูรณ์ของการรับรู้ ทำให้นักวิเคราะห์ต้องทำการ “ลากเส้นต่อจุด” โดยอาศัยประสบการณ์ของตนเองและข้อมูลข่าวสารเท่าที่มีอยู่ ณ ขณะนั้น

จากความล้าหลังและเกินจริงนี้ มูลค่าหุ้นที่คำนวณออกมา (เส้นประสีส้ม) จึงมีเฟสตามหลัง และมีแอมพลิจูด หรือขนาดของยอดคลื่น มากกว่าราคาหุ้นในโมเดลของเรา

จุดที่น่าสนใจ

เมื่อกำหนด A, B, C และ D เป็นจุดที่น่าสนใจบนโมเดล แล้วตั้งข้อสังเกตไล่ไปทีละจุด

ภาพขยายจุด A

เมื่อบริษัทมีกำไรเติบโตดี นักลงทุนก็ปรับมุมมองดีขึ้น ราคาหุ้น (เส้นสีฟ้า) จึงปรับตัวเพิ่มขึ้นมาเรื่อย ๆ จนถึงจุดหนึ่งที่พัฒนาการเชิงบวกของบริษัทเริ่มตีบตัน เช่น มีคู่แข่งเพิ่มขึ้น หรือเริ่มประสบปัญหาในการลดต้นทุน สถานการณ์เช่นนี้ทำให้นักลงทุนที่รู้จักบริษัทอย่างลึกซึ้งเริ่มระมัดระวัง และราคาหุ้นอาจชะลอตัว

อย่างไรก็ดี ตราบเท่าที่ตัวเลขผลการดำเนินงานยังไม่ประกาศออกมา นักลงทุนจำนวนมากย่อมคาดการณ์ผลกำไรของบริษัทโดยปรับแต่งตัวเลขจากอัตราการเติบโตของไตรมาสก่อน ๆ มูลค่าหุ้นที่ประเมินออกมาจึงมีแนวโน้มวิ่งต่อ ส่งผลให้เส้นประสีส้ม พุ่งทะยานแซงราคาหุ้นขึ้นไป

ลูกศรสีดำ แสดงให้เห็นว่า มูลค่าหุ้น ตามมุมมองของนักลงทุนขณะนั้น สูงกว่าราคาหุ้นปัจจุบัน จึงเปิดช่องให้กับมุมมองที่ว่า ราคาหุ้นอาจขยับตัวสูงขึ้นได้อีก (อยู่บนฐานความเชื่อที่ว่า เมื่อซื้อหุ้นได้ต่ำกว่ามูลค่าที่แท้จริง ที่สุดแล้วราคาหุ้นจะวิ่งขึ้นไปหามูลค่า) เพราะฉะนั้น ราคาหุ้นที่ปรับตัวขึ้นจนดูเหมือนว่าแพงมาตลอดทาง ก็อาจจะคุ้มค่ากับความเสี่ยง และไม่ควรเป็นปัญหาสำหรับหุ้นที่ “น่าซื้อ” ตัวนี้

ภาพขยายจุด B

นี่เป็นสถานการณ์ที่ราคาหุ้นปรับตัวลดลงจากจุดสูงสุดมาระยะหนึ่ง ทำให้หุ้นที่เคยแพงเริ่มดู “ไม่แพง” เมื่อเทียบกับช่วงเวลาก่อนหน้านั้น นักลงทุนอาจปรับลดมุมมองที่ดีเกินจริงลงมา คำนวณเป็นมูลค่าหุ้นก็ลดลงบ้าง แต่ถึงกระนั้นก็ยังคงสูงกว่าราคาหุ้นอยู่พอสมควร หลายคนจึงเข้าซื้อหุ้นเพื่อรอขายเมื่อราคาหุ้นวิ่งขึ้นไปหามูลค่า หรือถ้าเชื่อมั่นจริง ๆ ว่านี่เป็นซุปเปอร์สต็อก พวกเขาอาจเก็บหุ้นในจังหวะที่ราคาลดลงชั่วคราวและตั้งใจจะถือเอาไว้ตลอดไป

โดยสรุปก็คือ นี่เป็นหุ้นที่ถูกและน่าซื้อ เป็นสถานการณ์ที่หลายคนมองว่าค่อนข้างปลอดภัย หากจะซื้อหุ้นตัวนี้

ภาพขยายจุด C

หลังจากผลประกอบการที่ย่ำแย่ผลัดกันเวียนหน้าออกมาโชว์ต่อสาธารณะ ราคาหุ้นก็ไหลลงจนเรียกว่า ถูกแล้วถูกอีก นักลงทุนเองก็ปรับลดมุมมองครั้งแล้วครั้งเล่า จนมูลค่าหุ้นที่เคยสูงมุดลงต่ำกว่าราคาหุ้น กลายเป็นสถานการณ์ที่ราคาหุ้นขาดปัจจัยพื้นฐานรองรับ ในลักษณะนี้นักลงทุนที่มีเหตุมีผลอาจมองว่า ราคาหุ้นมีโอกาสลงต่อไปอีก

นั่นคือ หุ้นถูก แต่ก็ยังไม่น่าซื้ออยู่ดี

ภาพขยายจุด D

หลังจากตกต่ำอยู่พักใหญ่ ราคาหุ้นก็เริ่มทรงตัวและฟื้นขึ้นมาได้ อาจมีข่าวดีออกมาบ้าง แต่ก็ถือว่าเล็กน้อยเมื่อเทียบกับราคาหุ้นที่วิ่งขึ้น “อย่างไม่สมเหตุสมผล” หลายคนคิดว่าราคาหุ้นได้แพงจนสะท้อนข่าวดีพวกนั้นไปหมดแล้ว ฝ่ายผู้ที่คำนวณมูลค่าหุ้นแม้เห็นว่าบริษัทมีพัฒนาการอยู่บ้าง แต่ก็ไม่ถึงขั้นที่จะทัดเทียมกับราคาหุ้นที่วิ่งขึ้นมา

เมื่อหุ้นแพงเกินไปเทียบกับมูลค่าที่ยังกระเตื้องขึ้นไม่มาก บทสรุปของพวกเขาก็คือ ความฝันนั้นสวยหรูเกินจริง... แพง และไม่น่าซื้อด้วย

ถอยออกมา ช็อก!

ข้อสังเกตข้างต้นอยู่บนพื้นฐานของแต่ละจุดเวลา ซึ่งแน่นอนว่าหลายอย่างอาจเปลี่ยนไป หากเราถอยออกมามองภาพใหญ่

อย่างเช่น จุด A ที่หุ้นแพง + น่าซื้อ ความจริงกลับกลายเป็นว่าจุดนั้นเป็นฟองสบู่พอดี ส่วนจุด B ที่หุ้นถูก + น่าซื้อ แท้จริงหุ้นกำลังดิ่งเป็นขาลง

ขณะที่จุด C หุ้นถูก + ไม่น่าซื้อ แต่นั่นกำลังจะเป็นจุดต่ำสุดก่อนที่หุ้นจะฟื้นตัว และจุด D ที่หุ้นแพง + ไม่น่าซื้อ ที่จริงหุ้นกำลังอยู่ในขาขึ้น

พูดง่าย ๆ ว่ากลับหัวกลับหางไปหมด จุดที่คิดว่าน่าซื้อ ที่แท้ไม่ควรซื้อ ส่วนจุดที่คิดว่าไม่น่าซื้อ แต่ถ้าซื้อกลับมีกำไร นี่เป็นเรื่องน่าขันสำหรับผู้ที่พยายามจริงจังกับการลงทุน

...และขณะเดียวกันก็น่าปวดใจ

ผมเองก่อนหน้านี้ก็เคยซื้อหุ้นที่จุด B หรือหาจังหวะขายแถวจุด D ทำให้ขาดทุนไปบ้าง ชวดกำไรไปบ้าง ผลตอบแทนไม่ดีเท่าที่หวัง แต่ก็ไม่ทราบว่าผิดพลาดตรงไหน จนมาค้นพบตอนนี้

เมื่อนักลงทุนพยายามเลือกหุ้นที่มีความมั่นคง โดยมองจากความคงเส้นคงวาของกำไร 3-4 ปีล่าสุด พวกเขาอาจมองข้ามหรือปฏิเสธความเกี่ยวพันกับวัฏจักรไปได้ง่าย ๆ ทั้งที่ความเป็นวัฏจักรของหุ้นนั้นมีอยู่ทั่วไป ไม่ว่าจะเป็นวัฏจักรเศรษฐกิจ, วัฏจักรดอกเบี้ย, ค่าแรง, ค่าใช้จ่ายทุน (CAPEX) หรือราคาสินค้าโภคภัณฑ์ เป็นต้น และยิ่งความเป็นวัฏจักรชัดเจนขึ้นเท่าไร คำเตือนก็ยิ่งชัดเจนว่า...

หุ้นถูกไม่ใช่หุ้นน่าซื้อ และหุ้นน่าซื้อก็อาจไม่ใช่หุ้นน่าซื้อครับ

อธิบายความเร่งสู่ศูนย์กลาง

เมื่อแกว่งวัตถุเป็นวงกลม ทุกคนก็รู้จักว่าจะต้องมีความเร่งสู่ศูนย์กลาง

แต่ก็ไม่ค่อยรู้ว่าสูตรมีที่มาอย่างไร ในที่นี้ผมจะแสดงให้ดูตั้งแต่ต้นจนจบ ด้วยแนวคิดที่อาจแตกต่างไปจากที่หลาย ๆ ท่านเคยพบเห็นนะครับ

1. เริ่มจากรากฐาน

เมื่อพูดถึงการเคลื่อนที่แบบวงกลม เราก็ย่อมจะต้องมี รัศมี (r) และเส้นรอบวงซึ่งยาว 2πr เมื่อการเคลื่อนที่กวาดมุมไป ทำให้เกิดระยะทางบนเส้นโค้ง เราจะนิยาม มุม θ (theta - เทต้า) ว่าเท่ากับ ระยะทางบนเส้นโค้ง หารด้วย รัศมี ของวงกลม

อันนี้ไม่ต้องคิดมาก เพราะมันเป็นนิยามนะครับ ข้อสังเกตอันหนึ่ง คือ เมื่อกวาดมุมไปจนเกิดระยะทางยาวเท่ากับรัศมี r พอดี มุม θ ก็จะมีค่าเท่ากับหนึ่ง ซึ่งเรียกว่า 1 เรเดียน นั่นเอง

สมมติว่าการเคลื่อนที่ดังกล่าวใช้เวลา τ (tau หรือ เทา) หากเรานำ τ ไปหารทั้งสองข้าง จะได้ว่า

ฝั่งซ้าย  θ / τ  แท้จริงแล้วก็คือ ความเร็วที่กวาดมุมไปได้ในชั่วระยะเวลาหนึ่ง เรียกสิ่งนี้ว่า อัตราเร็วเชิงมุม ω (omega - โอเมกา) ส่วนฝั่งขวา ระยะทางบนเส้นโค้ง หารด้วย ระยะเวลา τ อันนี้เป็น อัตราเร็วเชิงเส้น v ที่เรารู้จักกัน

ดังนั้น

เป็นที่มาของสมการ  v = ω r  ที่หลายท่านเคยเรียนมาแล้ว

*** สมการข้างต้นนี้จะมีประโยชน์สำหรับการไขสูตรในลำดับต่อไป ***

2. เข้าไปยุ่งกับความเร็ว

เมื่อรากฐานแน่นแล้ว ต่อมาเราจะเข้าเรื่องโดยเข้าไปยุ่งกับจังหวะการเคลื่อนที่ไปบนวงกลมบ้าง

สมมติว่าจุดที่หนึ่งและจุดที่สอง วัตถุเคลื่อนที่ด้วยความเร็ว v₁ และ v₂ ตามลำดับ สังเกตว่าความเร็วมี ขนาด คงที่ เพียงแต่ ทิศทาง เท่านั้นที่เปลี่ยนไป

ต่อมาเราหยิบเฉพาะลูกศรที่แทนความเร็วมาพิจารณา เมื่อจับเอาหางลูกศรมาต่อกัน จะเห็นการเปลี่ยนแปลงความเร็ว (Δv) ซึ่งเป็น ลูกศรสีเขียว

หากลดทอนความวุ่นวายลงโดยตัดหัวลูกศรทั้งหมดออก แล้วพิจารณาเฉพาะ ขนาด จะเห็นเป็นรูปสามเหลี่ยมดังนี้

เมื่อนึกถึงความรู้เรขาคณิตพื้นฐาน สามเหลี่ยมที่มีด้านสองด้านยาวเท่ากัน เรียกว่า สามเหลี่ยมหน้าจั่ว ซึ่งเราจะสามารถ "แบ่งครึ่ง" ออกมาเป็นสามเหลี่ยมมุมฉากสองอัน โดยมุมยอด (θ) จะถูกหารสอง เช่นเดียวกันกับด้านฐาน (Δv) ก็จะถูกหารสองด้วยเช่นกัน

พอได้สามเหลี่ยมมุมฉาก เราก็สบายแล้ว เพราะว่าด้านที่อยู่ตรงข้ามมุม ( Δv / 2 ) จะมีค่าเท่ากับ v sin ( θ / 2 )

และเนื่องจากเรากำลังพิจารณาอัตราเร็ว ณ จุดใดจุดหนึ่งอยู่แล้ว มุม θ ก็ย่อมจะมีค่าน้อย ๆ ซึ่งในทางคณิตศาสตร์ sin (θ) จะมีค่าประมาณเท่ากับ θ

ประเด็นนี้ทุกท่านสามารถทดลองด้วยตนเองโดยกดเครื่องคิดเลข หรือค้นหาใน Google ระบุว่า "sin 0.02 radian" ผลลัพธ์จะออกมาประมาณ 0.019999 (ทั้งนี้ 0.02 เรเดียน เทียบเท่ามุม 1 องศานิด ๆ) แสดงว่า เมื่อมุมมีค่าน้อย sin (θ) จะมีค่าประมาณ θ นั่นเอง

ดังนั้น

ในบริบทที่มุม θ มีค่าน้อย เราอาจเขียนได้ว่า

ถึงตรงนี้ หากเรานำ τ ไปหารทั้งสองข้างของสมการ และอ้างอิงความรู้จากหัวข้อ 1. (เริ่มจากฐานราก) จะได้

ซึ่งอัตราเร็วที่เปลี่ยนแปลงไป (Δv) ในชั่วระยะเวลา τ  ก็คือ อัตราเร่งสู่ศูนย์กลาง

3. ส่งท้าย

ในความเป็นจริง การพิสูจน์อัตราเร่งสู่ศูนย์กลางสามารถทำได้หลายวิธี บางท่านใช้วิธีสามเหลี่ยมคล้าย หรือบางท่านอาจใช้แคลคูลัส แต่โดยส่วนตัวผมรู้สึกว่า วิธีที่แสดงไปข้างต้นนั้นค่อนข้างชัดเจน ตรงไปตรงมา และเป็นขั้นเป็นตอน

ที่สำคัญ คือ มัน "เจาะ" เข้าไปที่นิยามเลย วาดสามเหลี่ยมรูปเดียว ไม่ต้องเอาไปโยงกับใครให้เกิดความฉงนสงสัยตามมา จึงขอนำมาแบ่งปันด้วยประการฉะนี้

การ (ลงทุน) ตัดผมแบบเน้นมูลค่า

เมื่อผมเริ่มยาวจนรู้สึกรำคาญ มันก็หลีกเลี่ยงไม่ได้ที่จะต้อง “ตัดผม” แต่หลายท่านอาจนึกไม่ออกว่ากิจกรรมธรรมดาสามัญอย่างการตัดผมนี้จะสามารถเน้นมูลค่าได้อย่างไร

เริ่มต้นอย่างนี้ก็แล้วกันครับ สมมติว่าค่าตัดผม 100 บาท เป็นราคามาตรฐานในชุมชนของท่าน เมื่อตัดครั้งหนึ่งแล้วสามารถอยู่ไปได้เฉลี่ย 8 สัปดาห์ ก่อนจะทนไม่ไหวและต้องวิ่งกลับไปให้ช่างตัดอีกสักครั้ง

หากคิดในเชิงของนักลงทุน ค่าตัดผม 100 บาท ควรถือเป็นราคาที่ “ตลาด” ให้การยอมรับร่วมกัน ทั้งฝั่งลูกค้าและฝั่งร้านตัดผม ซึ่งก็แปลว่า คุณค่าที่ลูกค้าได้รับจากการตัดผมนั้น เทียบเท่าจำนวนเงิน 100 บาท ที่จ่ายไป

คุณค่าจากการได้ตัดผม

หลังตัดผมมาใหม่ ๆ เรามักรู้สึกพึงพอใจกับรูปลักษณ์และความเบาสบายศีรษะ จนครั้นเวลาผ่านไป เมื่อเส้นผมเริ่มชี้ไม่เป็นทรง หรือยาวขึ้นจนมาโดนหูโดนคอ ทำให้รู้สึกคันและหงุดหงิด

สิ่งหนึ่งที่ท่านน่าจะสังเกตได้ คือ ถึงแม้เส้นผมจะอยู่บนหัวของเราตลอด 8 สัปดาห์ (ก่อนจะไปตัดผมรอบใหม่) แต่คุณค่าในแต่ละสัปดาห์นั้นไม่เท่ากัน

สมมติคร่าว ๆ ว่าสัปดาห์ที่ 1-6 เป็นช่วงที่ผมเข้าทรง ทุกอย่างเรียบร้อยดี มีความสุข พอสัปดาห์ที่ 7 เริ่มหล่อน้อยลง ความสุขหดหาย แล้วพอสัปดาห์ที่ 8 ความทุกข์มาเยือนเต็มตัว หัวก็ฟู ทั้งร้อนทั้งคัน

หากแปลงให้เป็นเชิงปริมาณ (quantify) โดยกำหนดมูลค่าในแต่ละสัปดาห์ ดังนี้

จะเห็นว่าคุณค่าหรือมูลค่ารวมที่ได้รับ มีค่าเท่ากับเงินที่จ่ายค่าตัดผมพอดี นั่นคือ การตัดผมครั้งนี้ “เสมอตัว” เพราะท่านได้รับมูลค่ากลับมาเท่ากับจำนวนเงินที่จ่ายออกไป และโมเดลของเราก็สอดคล้องกับข้อสังเกตที่ได้กล่าวไปตั้งแต่ต้นว่า ราคาตลาด (ค่าตัดผม) ในปัจจุบันเป็นราคายุติธรรม หรือ fair price

ตัดผมแบบเน้นมูลค่า

ในกรณีที่ยืนพื้นตามโมเดลเดิม แต่ขยับกรอบเวลาการตัดผมให้สั้นลง เช่น จาก 8 สัปดาห์ ลดลงเหลือ 7 สัปดาห์ เราจะพบสิ่งที่น่าสนใจ

สังเกตว่าแม้ท่านจะจ่ายเงินค่าตัดผม 100 บาทเท่าเดิม แต่มูลค่ารวมที่ได้รับกลับเพิ่มขึ้นเป็น 120 บาท เพราะสัปดาห์สุดท้ายอันไม่น่าโสภาถูกกำจัดออกไป โดยแลกด้วย “รอบการตัดผม” ที่เวียนมาถึงเร็วขึ้น

เพื่อเปรียบเทียบกรอบเวลาการตัดผมทั้งสองแบบ

1. หากตัดผมทุก 8 สัปดาห์ ตลอดหนึ่งปีท่านจะตัดผมราว 6.5 ครั้ง เท่ากับเสียค่าตัดผม 6.5 x 100 = 650 บาท และได้มูลค่าจากการตัดผม 650 บาทเช่นกัน

2. หากตัดผมทุก 7 สัปดาห์ ตลอดหนึ่งปีท่านจะตัดผมราว 7.4 ครั้ง เท่ากับเสียค่าตัดผม 7.4 x 100 = 740 บาท

แม้การตัดผมทุก 7 สัปดาห์ จะทำให้ปีหนึ่ง ๆ เสียเงินมากขึ้น 740 – 650 = 90 บาท แต่ท่านไม่ต้องเผชิญ “ช่วงผมยาวรุงรัง” ที่น่ารำคาญ ซึ่งถ้าตัดผมไป 7.4 ครั้ง นั่นก็จะเท่ากับ 7.4 สัปดาห์ หรือประมาณปีละ 52 วัน ตีคร่าว ๆ ก็เกือบสองเดือนที่ชีวิตดีขึ้น แลกกับเงิน 90 บาท

ส่วนจะคุ้มหรือไม่สำหรับแต่ละท่าน ก็ลองพิจารณากันดูครับ

พาทัวร์ ROE

แม้ ROE จะเป็นอัตราส่วนทางการเงินตัวสำคัญที่อยู่ในความสนใจของนักลงทุน แต่ผู้คนที่มีความเข้าใจเชิงลึกกลับมีเพียงหยิบมือ ในบทความนี้ผมจะขอ “พาทัวร์” เพื่อให้ท่านได้รู้ได้เห็นตั้งแต่รากฐานจนถึงขั้นนำไปใช้งาน รวมทั้งพาชมอีกหลายสิ่งที่ชาวบ้านไม่ค่อยรู้ เพราะในหนังสือเขาไม่กล่าวถึงนะครับ

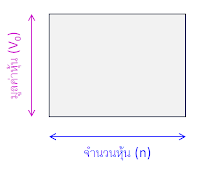
คำเรียกที่หลากหลาย

ตำราโดยมากมักบอกว่า Return on Equity (ROE) คือ อัตราผลตอบแทนต่อส่วนของผู้ถือหุ้น หรือบางเล่มอาจเรียกว่า อัตราผลตอบแทนจากส่วนของผู้ถือหุ้น หรือ อัตราผลตอบแทนสำหรับผู้ถือหุ้น และบางครั้งอาจลดทอนเหลือเพียง ผลตอบแทนต่อส่วนของผู้ถือหุ้น (ตัดคำว่า “อัตรา” ออกไป)

แต่ก็ขอให้เข้าใจว่า ทั้งหมดตั้งใจจะหมายความถึงสิ่งเดียวกัน นั่นคือ

ซึ่งที่จริงแล้วจะชัดเจนกว่า หากขยายความว่า

เมื่อบริษัทดำเนินกิจการและทำกำไรได้ กำไรส่วนหนึ่งจะถูกหักเป็น ดอกเบี้ยจ่าย ให้กับเจ้าหนี้ และจากนั้นก็หัก ภาษี ให้รัฐบาล จนทอดสุดท้ายเหลือเป็นกำไรส่วนที่มาถึงมือผู้ถือหุ้น ซึ่งเรียกว่า กำไรส่วนของผู้ถือหุ้น หรือ กำไรสุทธิ นั่นเอง

อันนี้เป็นคำอธิบายในฟากของ “ตัวเศษ” คือ กำไร

ถัดมาเป็นฟาก “ตัวส่วน” ซึ่งก็จะต้องสอดคล้องกัน เมื่อตัวเศษเป็นกำไรเฉพาะส่วนของผู้ถือหุ้น ตัวส่วนก็ต้องเป็นเงินทุนเฉพาะที่มาจากผู้ถือหุ้นเช่นกัน (เงินทุนที่มาจากทางอื่น เช่น เงินทุนที่ได้จากการกู้ยืมแบงก์หรือออกพันธบัตร เราจะไม่นับ)

สังเกตว่า ที่จริงแล้ว ROE ก็คือ อัตราผลตอบแทนที่คิดเป็นเปอร์เซ็นต์เทียบกับเงินทุนในรูปแบบหนึ่ง เป็นการไปดูว่าเงินทุนก้อนนั้น ๆ สามารถทำกำไรได้มากหรือน้อยอย่างไร ซึ่งนอกจาก ROE แล้วก็ยังมีอัตราส่วนตัวอื่นในทำนองเดียวกันนี้อีก เช่น ROCE และ ROIC (ทั้งสองตัวเป็นอัตราผลตอบแทนของ “เงินทุนรวม” ทั้ง เจ้าหนี้ + ผู้ถือหุ้น แตกต่างกันแค่ว่า ROIC นั้น ตัดเงินสดออกไป เพื่อเน้นเฉพาะเงินทุนส่วนที่มีการนำไปใช้ดำเนินงานจริง ๆ)

แต่เนื่องจากเราพุ่งความสนใจไปที่ เงินทุนจากผู้ถือหุ้น เป็นสำคัญ ดังนั้น ROE ก็นับว่าตรงงานที่สุดแล้ว

เงินทุน คือ สิ่งที่ต้องเน้น

หลายท่านอาจไม่ทราบว่า แท้จริงแล้วเมื่อเราซื้อหุ้น นั่นเท่ากับเรากำลัง “ซื้อเงินทุน” ส่วนของผู้ถือหุ้น

เงินทุนส่วนของผู้ถือหุ้น (Equity Capital) หากบันทึกในทางบัญชี จะเรียกว่า Book Value of Equity Capital หรือเวอร์ชันเต็มยศภาษาไทยว่า มูลค่าทางบัญชีของเงินทุนส่วนของผู้ถือหุ้น

แต่เพราะมันยาวไปกระมัง นักการเงินจึงมักเรียกสั้น ๆ แค่ Book Value (BV) เหมือนที่เราได้ยิน ส่วนนักบัญชีอาจมองว่าทุกอย่างในงบการเงินล้วนบันทึกเป็น book value หรือมูลค่าทางบัญชีอยู่แล้ว ดังนั้น เรียกว่า ส่วนของผู้ถือหุ้น (Equity) ก็พอ อันนี้ก็ว่ากันไป แต่ส่วนตัวแล้วผมมองว่าชื่อยาว ๆ นั่นแหละ สะท้อนความเป็นจริงได้ครบถ้วนครับ

หันกลับมาที่ตลาดหุ้นบ้าง เมื่อมีการนำเงินทุนนี้มาแบ่งเป็นหุ้น ๆ แล้วนำออกขาย เงินทุนก็จะมีราคาขึ้นมา เรียกว่า ราคาหุ้น (P) หรือหากท่านใดฟิตหน่อยจะเรียกเต็มยศว่า มูลค่าตลาดของเงินทุนส่วนของผู้ถือหุ้น ก็ได้ ยาวเหยียดและโก้ไปอีกแบบ

เมื่อมีทั้งตัว P และ BV แล้ว เราก็มักนำมาเทียบกันเป็นอัตราส่วน P/BV สมมติถ้าหุ้นตัวไหนมี P/BV = 2 ก็แสดงว่า เงินทุนนี้ซื้อขายกันด้วยราคาที่สูงเป็นสองเท่าของมูลค่าทางบัญชีที่บันทึกอยู่ในงบการเงิน อย่างนี้เป็นต้น

ข้อสังเกตเล็ก ๆ ที่ผมอยากชี้ให้เห็น คือ ในอัตราส่วน P/BV นั้น ทั้งตัวเศษและตัวส่วนต่างกล่าวถึงสิ่งเดียวกัน นั่นคือ เงินทุนส่วนของผู้ถือหุ้น เพียงแต่ตัวเศษเป็นมูลค่าตลาด (market value) ขณะที่ตัวส่วนเป็นมูลค่าทางบัญชี (book value)

ROE เป็นตัวผลักดัน P/BV จริงไหม?

การที่นักลงทุนเดินเข้าไปในตลาดหุ้นและยอมจ่ายแพงเมื่อเทียบกับมูลค่าทางบัญชี แสดงว่าเงินทุนนั้นจะต้องสร้างกำไรได้งามมาก (คือ ROE สูง) เป็นที่มาของการตั้งข้อสังเกตว่า ROE ของหุ้น น่าจะเป็นตัวผลักดันค่า P/BV ที่ตลาดยอมรับ

เราจะพิจารณาเรื่องนี้ผ่านสูตรของกอร์ดอน

เนื่องจาก เงินปันผล (D₁) เท่ากับ สัดส่วนการจ่ายเงินปันผล (d) คูณ กำไรต่อหุ้นในปีถัดไป (E₁) จึงเขียนใหม่ได้ว่า

จากนั้น นำ BV มาหารทั้งสองข้าง เพื่อให้ได้ค่า P/BV ที่เหมาะสม

สังเกตว่า E₁ / BV ก็คือ ค่า ROE นั่นเอง และสัดส่วนการจ่ายเงินปันผล (d) ก็เป็นส่วนที่เหลือจากกำไรที่จัดสรรเก็บเอาไว้ในบริษัท (b) ดังนั้น d = 1 - b และสมการข้างต้นจะสามารถเขียนได้ว่า

เนื่องจาก อัตราการเติบโตที่ยั่งยืน (sustainable growth rate) เป็นไปตามสมการ g = b x ROE ทำให้เขียนค่า P/BV ที่เหมาะสมได้ว่า

[หากสนใจที่มาของอัตราการเติบโตที่ยั่งยืน แนะนำให้เข้าไปศึกษาที่ https://mftfinance.wixsite.com/mftfinance/copy-of-gordonplus]

หากทดสอบสมการนี้ โดยกำหนดให้ r = 10% และ g = 5% จากนั้นดูความสัมพันธ์ระหว่าง P/BV และ ROE จะได้แผนภาพ

ซึ่งยืนยันว่าค่า ROE เป็นตัวผลักดันมูลค่า (value driver) ผ่าน P/BV ที่เหมาะสมของหุ้น และหากท่านใดขยันหน่อย จัดรูปสมการดี ๆ ก็จะได้รูปแบบ y = mx + c ซึ่งแสดงความสัมพันธ์แบบเส้นตรง

ตัวกำหนดเขตแดน

เมื่อสังเกตสมการ

กรณีที่ ROE มีค่าเท่ากับอัตราผลตอบแทนที่ผู้ถือหุ้นคาดหวัง (ROE = r) พอดี ตัวเศษ และ ตัวส่วน ด้านขวาของสมการจะมีค่าเท่ากัน ทำให้ P/BV เท่ากับหนึ่ง

สมมติคราวนี้เราสร้างแผนภาพใหม่ เป็นความสัมพันธ์ระหว่าง ราคาหุ้น (P) และมูลค่าทางบัญชี (BV) แทน เราจะได้เส้นตรง P = BV ดังรูปซ้าย

นี่เป็นเส้นตรงที่แบ่งเขตแดนความชอบธรรม ระหว่างหุ้นที่มี ROE สูงและ ROE ต่ำ เมื่อเทียบกับอัตราผลตอบแทนคาดหวังของผู้ถือหุ้น (r) ซึ่งรูปขวาจะทำให้ท่านเห็นสิ่งนี้ได้ชัดเจนขึ้น

รูปนี้แสดงให้เห็นว่า แนวคิดดั้งเดิมของ VI ที่นิยมซื้อหุ้น P/BV ต่ำ (เช่น ไม่เกินหนึ่งเท่า) มีแนวโน้มจะทำให้ซื้อหุ้นที่มี ROE ต่ำไปด้วย หรือพูดอีกอย่างก็คือ ไปซื้อหุ้นที่ใช้เงินทุนมาก แต่สร้างกำไรได้น้อย ซึ่งไม่ค่อยดีเท่าไรในเชิงคุณภาพ แนวคิดนี้จึงค่อย ๆ ถูกแทนที่ด้วยองค์ความรู้ใหม่ที่ได้รับการพัฒนาขึ้นในระยะหลัง

แล้ว ROE เป็นตัวผลักดัน P/E ด้วยไหม?

โดยมากแล้วเรามักยอมรับกันว่า P/E ของหุ้นถูกผลักดันด้วยอัตราการเติบโต (g) กล่าวคือ ถ้า g สูง ตลาดก็จะยอมรับค่า P/E ที่สูงขึ้น อย่างไรก็ตาม หากเราจัดสูตรของกอร์ดอนใหม่อีกรอบ เพื่อหาค่า Forward P/E ที่เหมาะสม

และสุดท้ายจัดรูป ตัวส่วน ให้เป็นทรงเดียวกับ ตัวเศษ

จะเห็นว่าในสมการสุดท้ายนี้ กรณีฐาน ที่ ROE = r พอดี ตัวเศษ และ ตัวส่วน ในวงเล็บก้ามปู จะมีค่าเท่ากัน ทำให้ P/E ลดรูปเหลือเพียง

ถัดมาเพื่อให้เห็นภาพชัดเจนขึ้น เราพล็อตความสัมพันธ์ระหว่าง P/E และ ROE โดยกำหนดให้ r = 10% และ g = 5% เช่นเดิม แผนภาพแสดงให้เห็นว่า เมื่อหุ้นมี ROE สูงขึ้น ตลาดก็จะยอมรับ P/E ที่สูงขึ้นเช่นกัน แต่ความสัมพันธ์นั้นไม่ได้เป็นไปแบบเส้นตรง

จุดที่ควรสังเกต คือ เมื่อ ROE = r (คือ 10 เปอร์เซ็นต์) เป็นกรณีฐาน P/E ของหุ้นจะอยู่ที่เศษหนึ่งส่วน r หรือ 1 / 0.10 = 10 เท่า ตรงจุดสีน้ำเงิน จากนั้นเมื่อ ROE สูงขึ้น P/E ก็ปรับตัวเพิ่มขึ้นไปทางลูกศรสีเขียว และเมื่อ ROE น้อยลง P/E ก็ปรับตัวลดลงไปทางลูกศรสีเหลือง

ด้วยเหตุนี้ หากจะตอบคำถามที่ว่า ROE เป็นตัวที่ผลักดัน P/E ของหุ้นด้วยไหม ก็คงต้องบอกว่า ใช่ แต่การผลักดันนี้ก็มีขอบเขตของมัน พิจารณาจากสมการข้างต้น

ใช้วิชาแคลคูลัส (ที่หลายท่านชอบบ่นว่าไม่รู้จะเรียนไปทำไม) มาหาค่าขอบเขต หรือ limit เมื่อ ROE มีค่ามากจนเข้าใกล้อนันต์

นั่นคือ ไม่ว่าบริษัทจะมีค่า ROE สูงเพียงใด ค่า P/E ก็ไม่ควรสูงเกินกว่าเศษหนึ่งส่วน r - g ซึ่งในกรณีตัวอย่างของเรา 1 / (0.10 – 0.05) = 20 เท่า นั่นเอง

อยากรวยต้องซื้อหุ้น ROE สูงจริงไหม

ตอบแบบสั้น ๆ ว่า ไม่จริง

ตอบแบบยาวหน่อยผ่านตัวอย่างหุ้นสองตัวที่มีมูลค่าทางบัญชี 20 บาทเท่ากัน โดยหุ้น A มีค่า ROE = 20% และหุ้น B มีค่า ROE = 8%

ด้วยคุณลักษณะนี้ สมมติคำนวณออกมาได้ว่า หุ้น A มีมูลค่า 60 บาท และหุ้น B มีมูลค่า 12 บาท ในสถานการณ์ที่ตลาดหุ้นตื่นตระหนก ท่านสามารถซื้อหุ้นทั้งสองตัวได้ ณ ราคาเพียง “ครึ่งหนึ่ง” ของมูลค่า และขายเมื่อราคาดีดกลับขึ้นไปเท่ามูลค่าหุ้น

เท่ากับว่าได้กำไร 100 เปอร์เซ็นต์ ไม่ว่าเลือกซื้อหุ้นตัวไหน

เพราะฉะนั้น ROE ที่สูงและต่ำ เพียงแค่กำหนดว่ามูลค่าหุ้นควรอยู่ที่จุดไหน (เมื่อเทียบกับ BV) เหมือนคำพูดที่ว่า “หุ้นทุกตัวล้วนมีราคาที่เหมาะสมของมัน” แต่กำไรที่จะได้นั้นขึ้นอยู่กับความได้เปรียบที่ท่านเลือกเองในการ ซื้อ-ถือ-ขาย ให้สอดคล้องกับธรรมชาติของหุ้นแต่ละตัว

ทั้งนี้ นักลงทุนต้องไม่สับสนระหว่างการหามูลค่าหุ้นกับการหาความได้เปรียบภายหลังจากที่ทราบมูลค่าหุ้นแล้ว ซึ่ง ROE จะมีบทบาทในข้อแรก (การหามูลค่าหุ้น) ไม่ใช่ข้อหลัง

สรุป คือ ถ้าทำได้ถูกต้อง ทั้งหุ้น ROE สูง และหุ้น ROE ต่ำ ล้วนพาท่านไปสู่ความมั่งคั่งได้ทัดเทียมกัน

ความสามารถในการต้านทานความผิดหวัง

แม้โอกาสสร้างกำไรมีอยู่ในหุ้นทั้งสองแบบ แต่ท่านนักลงทุนก็พึงทราบว่าหุ้น ROE สูง และหุ้น ROE ต่ำ จะตอบสนองต่อความผันแปรได้แตกต่างกัน

สมมติต่อเนื่องจากตัวอย่างเดิม เมื่อหุ้นทั้งสองตัวต่างประสบปัญหาจนความสามารถในการทำกำไร (และ ROE) ลดลงหนึ่งในสี่ คือ ลดลงจาก 20% เหลือ 15% ในกรณีหุ้น A และลดลงจาก 8% เหลือ 6% ในกรณีหุ้น B

เมื่อคำนวณมูลค่าหุ้น (โดยใช้ค่า r = 10% และ g = 5%) หุ้น A จะมีมูลค่าลดลงจาก 60 บาท เหลือ 40 บาท ส่วนหุ้น B มีมูลค่าลดลงจาก 12 บาท เหลือ 4 บาท

ดังนั้น ขณะที่หุ้น A มีมูลค่าลดลง 33 เปอร์เซ็นต์ ซึ่งก็แย่แล้ว แต่หุ้น B กลับลดลงถึง 67 เปอร์เซ็นต์ นับว่าเข้าข่ายหายนะเลยก็ว่าได้ นี่คือความแตกต่างในการรักษามูลค่าเอาไว้ เมื่อผลประกอบการเสื่อมถอย

พูดให้ชัดก็คือ มูลค่าของหุ้น ROE สูง มักมีความเสถียรมากกว่าหุ้น ROE ต่ำ

อย่างไรก็ตาม ก่อนที่ท่านจะกระโดดหนีหุ้น ROE ต่ำไปเลย ผมอยากให้ลองคิดในทางตรงข้ามด้วย สมมติกลับกัน คือ หุ้นทั้งสองฟื้นตัวหรือมีความสามารถในการทำกำไรเพิ่มขึ้น คราวนี้หุ้น ROE ต่ำจะมีมูลค่าสูงขึ้นอย่างก้าวกระโดด ในขณะที่หุ้น ROE สูง อาจมีมูลค่าเพิ่มขึ้นไม่มากนัก

ด้วยเหตุนี้ นักลงทุนที่คาดหวังผลตอบแทนดี ๆ จากการซื้อหุ้น P/BV ต่ำ (ซึ่งก็มักมี ROE ต่ำด้วย) จึงต้องมีคุณลักษณะสำคัญ คือ สามารถ “อ่านทิศทาง” ผลประกอบการของบริษัทได้แม่นและเร็วกว่านักลงทุนทั่วไป

--------------------------------------

จากที่ได้พาทัวร์ ROE มาจนถึงตรงนี้ หวังว่าทุกท่านจะได้รับสาระและความบันเทิง (?!) ตลอดจนแนวคิดใหม่ ๆ เป็นประโยชน์ต่อการลงทุนโดยทั่วกันครับ

มูลค่าของหุ้นวัฏจักร

นักลงทุนจำนวนมากบอกว่า หุ้นวัฏจักร ประเมินมูลค่าได้ยาก ทำไปก็เสี่ยงเข้ารกเข้าพง แม้ในตำราวีไอฉบับไทย ๆ ก็ไม่ค่อยมีใครประเมินกัน อย่างไรก็ตาม หากเราไปดูตำราต่างประเทศ ก็จะพบว่าวิธีนั้นมีอยู่

แต่ก่อนจะไปถึงตรงนั้น ต้องทำความเข้าใจธรรมชาติของหุ้นประเภทนี้เสียก่อน

ธรรมชาติของหุ้นวัฏจักร

หุ้นวัฏจักร เป็นหุ้นที่มีช่วงเวลาดี ๆ สลับกับช่วงเวลาแย่ ๆ กำไรต่อหุ้น (EPS) จึงไม่ค่อยเติบโตต่อเนื่อง แต่อาจเป็นไปทำนองนี้

สังเกตว่าในตัวอย่างของเรา กำไรมีการขึ้น ๆ ลง ๆ แบบรูปคลื่นพื้นฐาน [เส้นโค้งสีน้ำเงิน] ซึ่งที่จริงหากถอยออกมามองภาพใหญ่ กำไรเฉลี่ยในระยะยาวยังมีแนวโน้มเติบโตขึ้นอย่างช้า ๆ [เส้นประสีดำ]

ในโลกความจริง ช่วงเฟื่องฟูและช่วงตกต่ำอาจไม่ชัดเจนเหมือนแบบจำลองของเรา แต่ถึงกระนั้น การหา “ระดับกำไรปกติ” จากค่าเฉลี่ยย้อนหลังไปหลาย ๆ ปี โดยให้ครอบคลุมตลอดช่วงวัฏจักร ก็ยังอยู่ในวิสัยที่ทำได้

เมื่อทราบแนวโน้มการเติบโตของกำไรปกติในระยะยาว [เส้นประสีดำ] และอนุมานว่าเงินปันผล รวมถึงกระแสเงินสดต่าง ๆ มีความสอดคล้องกับกำไรปกติดังกล่าว คราวนี้การประเมินมูลค่าหุ้นก็ไม่มีอะไรซับซ้อนแล้ว มูลค่าหุ้นอย่างคร่าว ๆ ก็จะเป็นไปตาม [เส้นประสีแดง] นั่นเอง

มูลค่าหุ้นอย่าง ไม่ คร่าว

หากนักลงทุนก้าวไปอีกขั้น โดยนำการขึ้น ๆ ลง ๆ ของกำไร (และกระแสเงินสด) มาคำนวณมูลค่าหุ้นด้วยการคิดลดกระแสเงินสดบนโปรแกรม Excel มูลค่าหุ้นก็จะออกมาเป็นลูกคลื่น ดังภาพ

ทั้งนี้ ท่านนักลงทุนอาจสังเกตได้ว่า “ยอดคลื่น” ของกำไรกับมูลค่าหุ้นนั้นเหลื่อมกันอยู่ เช่น ยอดคลื่นของมูลค่าหุ้น [ลูกศรสีเหลือง] ตรงกับปีที่ 8 แต่ยอดคลื่นของกำไร [ลูกศรสีเขียว] กลับไปตรงกับปีที่ 10

เพราะฉะนั้น ในรอบวัฏจักร 8 ปีนี้ มูลค่าหุ้นจะ นำหน้า กำไรอยู่ราว 2 ปี หรือเศษหนึ่งส่วนสี่ของรอบวัฏจักร ซึ่งเฟสของคลื่นที่เหลื่อมหรือไม่ตรงกันดังกล่าว มีผลทำให้การลงทุนหุ้นวัฏจักรกลายเป็นเรื่องยากและฝืนสามัญสำนึกขึ้นมา

เหตุผลที่ยาก

ประการแรก นักลงทุนมีความคุ้นเคยกับหุ้นกลุ่มอื่น ๆ ซึ่งมีธรรมชาติแตกต่างจากหุ้นวัฏจักรนับเป็นเวลาช้านาน พวกเขาซึมซับความคิดที่ว่า

กำไรดี = มูลค่าสูง

และ

กำไรแย่ = มูลค่าต่ำ

เมื่อพบว่ากรอบความคิดเดิมใช้งานไม่ได้ พวกเขาจึงเริ่มสับสน

ประการที่สอง การ “เหลื่อมเฟส” ของกำไรกับมูลค่าหุ้นเพียง 90 องศา (เศษหนึ่งส่วนสี่ของรอบวัฏจักร) รับมือได้ยากกว่าการคิดแบบกลับหัวกลับหาง 180 องศา เช่น สูงกลายเป็นต่ำ หรือ ดีกลายเป็นแย่

ประการที่สาม การตีความอัตราส่วนที่เกี่ยวข้องกับการตัดสินใจลงทุน เช่น P/E ในกรณีของหุ้นวัฏจักร มีความแตกต่างออกไป

สังเกตว่าช่วงที่มูลค่าหุ้นเป็นขาขึ้น [ลูกศรสีเขียว] จะตรงกับช่วงที่กำไรถดถอยอย่างน่ากลัว ผลักดันค่า P/E ให้สูงลิบลิ่วจนดูเหมือนหุ้นมีราคาแพง ไม่น่าซื้อ

ในทางกลับกัน ช่วงที่มูลค่าหุ้นเป็นขาลง [ลูกศรสีชมพู] ตรงกับช่วงที่บริษัทมีกำไรสูงทำลายสถิติ ซึ่งก็จะดึงให้ค่า P/E ลดลงจนดูเหมือนหุ้นมีราคาถูก ปลอดภัย และกลายเป็น “กับดัก” ที่ทำให้หลายคนติดหุ้นวัฏจักรในช่วงขาลง

บทสรุป

แม้หุ้นวัฏจักรจะประเมินมูลค่าได้ยากกว่าปกติ ทว่าเป็นโอกาสดีสำหรับคนที่รู้จริง (และใจกล้าพอ!) เพราะว่ามีคนในตลาดมากมายพร้อมจะโยนเงินทิ้งในจังหวะที่ท่านรู้ดีว่าควรเข้าไปเก็บ

ข้อสำคัญที่ต้องตระหนักก็คือ หุ้นพวกนี้ซื้อแล้วต้องขายให้เป็นด้วย ไม่อย่างนั้นอาจได้ถือยาวจนครบรอบวัฏจักร